题目内容
已知向量a=(cosλθ,cos(10-λ)θ),b=(sin(10-λ)θ,sinλθ),λ、θ∈R.
(1)求|a|2+|b|2的值;
(2)若a⊥b,求θ;
(3)若θ=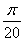 ,求证:a∥b.
,求证:a∥b.
(1)2(2)θ=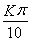 (3)见解析
(3)见解析
【解析】(1)解:∵|a|= ,
,
|b|= ,
,
∴|a|2+|b|2=2.
(2)解:∵a⊥b,
∴cosλθ·sin(10-λ)θ+cos(10-λ)θ·sinλθ=0,
∴sin[(10-λ)θ+λθ]=0,∴sin10θ=0,
∴10θ=kπ,k∈Z,∴θ=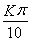 ,k∈Z.
,k∈Z.
(3)证明:∵θ=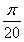 ,
,
cosλθ·sinλθ-cos(10-λ)θ·sin[(10-λ)θ]
=cos ·sin
·sin -cos
-cos ·sin
·sin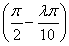
=cos ·sin
·sin -sin
-sin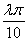 ·cos
·cos =0,∴a∥b
=0,∴a∥b

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目