题目内容
【题目】已知集合A={x|0＜ax+1≤5}，B={x|﹣ 
＜x≤2}．
（1）当a=1时，判断集合BA是否成立？
（2）若AB，求实数a的取值范围．
【答案】
（1）解：当a=1时，集合A={x|0＜x+1≤5}={x|﹣1＜x+1≤4}，B={x|﹣ 
＜x≤2}．
∴BA成立
（2）解：当a=0时，A=R，AB不成立；
当a＜0时，A={x|0＜ax+1≤5}={x| 
≤x＜ 
}，
若AB，则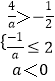 
，解得：a＜﹣8；
当a＞0时，A={x|0＜ax+1≤5}={x| ＜x≤ }，
若AB，则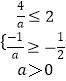 
，解得：a≥2；
综上可得：a＜﹣8，或a≥2
【解析】（1）当a=1时，集合A={x|0＜x+1≤5}={x|﹣1＜x+1≤4}，根据集合包含关系的定义，可得结论；（2）根据集合包含关系的定义，对a进行分类讨论，最后综合，可得满足条件的实数a的取值范围．
练习册系列答案
相关题目
