题目内容
【题目】若定义在区间D上的函数y=f(x)满足:对x∈D,M∈R,使得|f(x)|≤M恒成立,则称函数y=f(x)在区间D上有界.则下列函数中有界的是: .
①y=sinx;② ![]() ;③y=tanx;④
;③y=tanx;④ ![]() ;
;
⑤y=x3+ax2+bx+1(﹣4≤x≤4),其中a,b∈R.
【答案】①④⑤
【解析】解:①∵y=|sinx|≤1,
∴函数y=|sinx|在区间R上有界.
②∵y=|x+ ![]() |≥2
|≥2
∴函数y=|x+ ![]() |在区间{x|x≠0}上无界;
|在区间{x|x≠0}上无界;
③∵y=|tanx|≥0
∴函数y=|tanx|在区间{x|x≠ ![]() +kπ,k∈Z}上无界;
+kπ,k∈Z}上无界;
④∵ ![]() ;
;
令t=ex , t>0
则原式y= ![]() =1﹣
=1﹣ ![]() ∈(﹣1,1)
∈(﹣1,1)
即值域为(﹣1,1)
∴存在M=1,对x∈R,使得|f(x)|≤M恒成立,
∴④是有界的.
⑤∵y=x3+ax2+bx+1(﹣4≤x≤4),
∴y在区间[﹣4,4]上是连续的函数,故一定要最大值P和最小值Q,
设M=max{|P|,|Q|}
∴对x∈D,M∈R,使得|f(x)|≤M恒成立,
故⑤是有界的.
故本题答案为:①④⑤.
【考点精析】关于本题考查的函数的最值及其几何意义,需要了解利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能得出正确答案.

 应用题作业本系列答案
应用题作业本系列答案【题目】目前我国城市的空气污染越来越严重,空气质量指数![]() 一直居高不下,对人体的呼吸系统造成了严重的影响,现调查了某城市500名居民的工作场所和呼吸系统健康,得到
一直居高不下,对人体的呼吸系统造成了严重的影响,现调查了某城市500名居民的工作场所和呼吸系统健康,得到![]() 列联表如下:
列联表如下:
室外工作 | 室内工作 | 合计 | |
有呼吸系统疾病 | 150 | ||
无呼吸系统疾病 | 100 | ||
合计 | 200 |
(Ⅰ)请把![]() 列联表补充完整;
列联表补充完整;
(Ⅱ)你是否有95%的把握认为感染呼吸系统疾病与工作场所有关;
(Ⅲ)现采用分层抽样从室内工作的居民中抽取一个容量为6的样本,将该样本看成一个总体,从中随机抽取2人,求2人都有呼吸系统疾病的概率.
参考公式与临界表:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】微信红包是一款可以实现收发红包、查收记录和提现的手机应用.某网络运营商对甲、乙两个品牌各5种型号的手机在相同环境下抢到的红包个数进行统计,得到如下数据:
手机品牌 型号 | I | II | III | IV | V |
甲品牌(个) | 4 | 3 | 8 | 6 | 12 |
乙品牌(乙) | 5 | 7 | 9 | 4 | 3 |
手机品牌 红包个数 | 优 | 非优 | 合计 |
甲品牌(个) | |||
乙品牌(个) | |||
合计 |
(1)如果抢到红包个数超过5个的手机型号为“优”,否则为“非优”,请完成上述2×2列联表,据此判断是否有85%的把握认为抢到的红包个数与手机品牌有关?
(2)如果不考虑其他因素,要从甲品牌的5种型号中选出3种型号的手机进行大规模宣传销售.
①求在型号I被选中的条件下,型号II也被选中的概率;
②以![]() 表示选中的手机型号中抢到的红包超过5个的型号种数,求随机变量
表示选中的手机型号中抢到的红包超过5个的型号种数,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
下面临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: 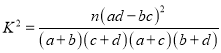 ,其中
,其中![]() .
.