题目内容
【题目】如下图,在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,则直线D1E与A1D所成角的大小是 , 若D1E⊥EC,则直线A1D与平面D1DE所成的角为 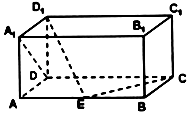
【答案】90°;30°
【解析】解:∵在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,∴以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,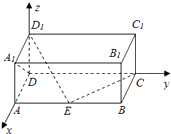
则D(0,0,0),D1(0,0,1),A(1,0,0),A1(1,0,1),C(0,2,0),
设E(1,t,0),0≤t≤2,
则 ![]() =(1,t,﹣1),
=(1,t,﹣1), ![]() =(﹣1,0,﹣1),
=(﹣1,0,﹣1),
∴ ![]()
![]() =﹣1+0+1=0,
=﹣1+0+1=0,
∴直线D1E与A1D所成角的大小是90°.
∵ ![]() =(1,t,﹣1),
=(1,t,﹣1), ![]() =(﹣1,2﹣t,0),D1E⊥EC,
=(﹣1,2﹣t,0),D1E⊥EC,
∴ ![]()
![]() =﹣1+t(2﹣t)+0=0,
=﹣1+t(2﹣t)+0=0,
解得t=1,∴AE=1.
平面D1DE的法向量为 ![]() =(﹣1,1,0),cos<
=(﹣1,1,0),cos< ![]() ,
, ![]() >=
>= ![]() =﹣
=﹣ ![]() ,
,
∴直线A1D与平面D1DE所成的角为30°.
所以答案是90°,30°.
【考点精析】本题主要考查了异面直线及其所成的角和空间角的异面直线所成的角的相关知识点,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则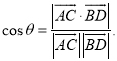 才能正确解答此题.
才能正确解答此题.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案【题目】目前我国城市的空气污染越来越严重,空气质量指数![]() 一直居高不下,对人体的呼吸系统造成了严重的影响,现调查了某城市500名居民的工作场所和呼吸系统健康,得到
一直居高不下,对人体的呼吸系统造成了严重的影响,现调查了某城市500名居民的工作场所和呼吸系统健康,得到![]() 列联表如下:
列联表如下:
室外工作 | 室内工作 | 合计 | |
有呼吸系统疾病 | 150 | ||
无呼吸系统疾病 | 100 | ||
合计 | 200 |
(Ⅰ)请把![]() 列联表补充完整;
列联表补充完整;
(Ⅱ)你是否有95%的把握认为感染呼吸系统疾病与工作场所有关;
(Ⅲ)现采用分层抽样从室内工作的居民中抽取一个容量为6的样本,将该样本看成一个总体,从中随机抽取2人,求2人都有呼吸系统疾病的概率.
参考公式与临界表:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |