题目内容
【题目】已知函数f(x)=loga(x2﹣2ax)(a>0且a≠1)满足对任意的x1 , x2∈[3,4],且x1≠x2时,都有 ![]() >0成立,则实数a的取值范围是
>0成立,则实数a的取值范围是
【答案】(1, ![]() )
)
【解析】解:∵对任意的x1 , x2∈[3,4],且x1≠x2时,都有 ![]() >0成立,
>0成立,
∴函数f(x)=loga(x2﹣2ax)(a>0且a≠1)在[3,4]上为增函数,
当a∈(0,1)时,y=logat为减函数,t=x2﹣2ax,x∈[3,4]为增函数,
此时函数f(x)=loga(x2﹣2ax)(a>0且a≠1)不可能为增函数,
当a∈(1,+∞)时,y=logat为增函数,
若函数f(x)=loga(x2﹣2ax)(a>0且a≠1)在[3,4]上为增函数,
则t=x2﹣2ax,x∈[3,4]为增函数,且恒为正,
即 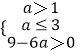 ,
,
解得:a∈(1, ![]() ),
),
所以答案是:(1, ![]() )
)
【考点精析】本题主要考查了复合函数单调性的判断方法的相关知识点,需要掌握复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”才能正确解答此题.

练习册系列答案
相关题目