题目内容
【题目】已知圆![]() ,
, ![]() 在抛物线
在抛物线![]() 上,圆
上,圆![]() 过原点且与
过原点且与![]() 的准线相切.
的准线相切.
(Ⅰ) 求![]() 的方程;
的方程;
(Ⅱ) 点![]() ,点
,点![]() (与
(与![]() 不重合)在直线
不重合)在直线![]() 上运动,过点
上运动,过点![]() 作
作![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
, ![]() .求证:
.求证: ![]() (其中
(其中![]() 为坐标原点).
为坐标原点).
【答案】(I)![]() ;(Ⅱ) 见解析.
;(Ⅱ) 见解析.
【解析】试题分析:(I)原点在圆上,抛物线准线与圆相切,可得![]() 三者之间的关系,进而求出
三者之间的关系,进而求出![]() 的方程;(Ⅱ) 设
的方程;(Ⅱ) 设![]() ,
, ![]() ,
, ![]() ,利用导数求得两切线方程,利用根与系数关系可证
,利用导数求得两切线方程,利用根与系数关系可证![]() ,即证两角相等.
,即证两角相等.
试题解析:(I)解法一:因为圆![]() 的圆心在抛物线上且与抛物线的准线相切,且圆半径为
的圆心在抛物线上且与抛物线的准线相切,且圆半径为![]() ,
,
故![]() ,
,
因为圆过原点,所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,所以抛物线
,所以抛物线![]() 方程
方程![]() .
.
解法二:因为圆![]() 的圆心在抛物线上且与抛物线的准线相切,由抛物线的定义,
的圆心在抛物线上且与抛物线的准线相切,由抛物线的定义,
圆![]() 必过抛物线的焦点
必过抛物线的焦点![]() ,
,
又圆![]() 过原点,所以
过原点,所以![]() ,
,
又圆的半径为3,所以![]() ,又
,又![]() ,
,
又![]() ,得
,得![]() ,所以
,所以![]() .所以抛物线
.所以抛物线![]() 方程
方程![]() .
.
解法三:因为圆![]() 与抛物线准线相切,所以
与抛物线准线相切,所以![]() ,
,
且圆过![]() 又圆过原点,故
又圆过原点,故![]() ,可得
,可得![]() ,
,
解得![]() ,所以抛物线
,所以抛物线![]() 方程
方程![]()
(Ⅱ) 解法一:设![]() ,
, ![]() ,
, ![]() ,
, ![]() 方程为
方程为![]() ,所以
,所以![]() , 5分
, 5分
求得抛物线在点![]() 处的切线的斜率
处的切线的斜率![]() ,所以切线
,所以切线![]() 方程为:
方程为: ![]() ,
,
即![]() ,化简得
,化简得![]() ,
,
又因过点![]() ,故可得,
,故可得, ![]() ,
,
即![]() ,同理可得
,同理可得![]() ,
,
所以![]() 为方程
为方程![]() 的两根,所以
的两根,所以![]() ,
, ![]() ,
,
因为![]() ,所以
,所以![]() ,
,
化简![]()
![]() .
.
所以![]() .
.
解法二:依题意设点![]() ,设过点
,设过点![]() 的切线为
的切线为![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,即
,即![]() ,
,
不妨设切线![]() 的斜率为
的斜率为![]() ,点
,点![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,又
,又![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,
, ![]() ,即点
,即点![]() ,同理点
,同理点![]() ,
,
因为![]() ,所以
,所以![]() ,同理
,同理![]() ,
,
所以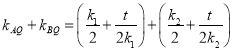
![]()
![]() ,
,
所以![]() .
.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目