题目内容
9.计算:已知tanα,tanβ是方程x2-3x-3=0的两根,求sin2(α+β)的值.分析 利用韦达定理以及两角和的正切函数,通过万能公式求解即可.
解答 (本小题满分12分)
〔解〕∵tanα,tanβ是方程x2-3x-3=0的两根,
∴tanα+tanβ=3,tanα•tanβ=-3…(4分)
∴$tan(α+β)=\frac{tanα•+tanβ}{1-tanα••tanβ}=\frac{3}{4}$…(7分)
∴$sin2(α+β)=\frac{2tg(α+β)}{{1-t{g^2}(α+β)}}=\frac{24}{25}$.…(12分)
点评 本题考查两角和的正切函数的应用,考查三角函数的化简求值,是基础题.

练习册系列答案
相关题目
20.设f(x)=$\frac{1}{3}{x^3}+a{x^2}$+5x+6在区间[1,3]上为单调函数,则实数a的取值范围是( )
| A. | [-$\sqrt{5}$,+∞) | B. | (-∞,-3] | C. | (-∞,-3]∪[-$\sqrt{5}$,+∞) | D. | [-$\sqrt{5}$,$\sqrt{5}$] |
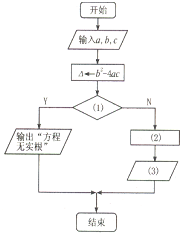 如图是求解一元二次方程ax2+bx+c=0(a≠0)的流程图,根据题意填写:
如图是求解一元二次方程ax2+bx+c=0(a≠0)的流程图,根据题意填写: