题目内容
【题目】已知
是圆
外一点，过点
作圆
的切线，切点为
，记四边形
的面积为
，当
在圆
上运动时， 
的取值范围为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】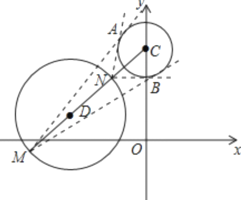
由题意得到圆心
，半径
；圆心
，半径
， 
， 
，当
位于图形中的
位置时，四边形
面积最小，过
作圆
的切线，切点分别为
，连接
，可得出
，且
，则
中，根据勾股定理得： 
，此时
，当
位于图形中的
位置时，四边形
面积最大，同理得到
，综上， 
的范围为
，故选A.
【方法点晴】本题主要考查圆的方程、直线与圆的位置关系以及求取值范围问题，属于难题.解决圆解析几何中的取值范围问题一般有两种方法：一是几何意义，特别是用圆锥曲线的定义和平面几何的有关结论来解决，非常巧妙；二是将圆解析几何中取值范围问题转化为函数问题，然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法，本题利用圆的几何性质求三角形面积最值的.
练习册系列答案
相关题目
【题目】某种产品的广告费支出
(百万元)与销售额
(百万元)之间有如下对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 50 | 60 | 70 |
如果
与
之间具有线性相关关系.
（1）作出这些数据的散点图；
（2）求这些数据的线性回归方程
;
（3）预测当广告费支出为9百万元时的销售额。 ( 参考数据： 
)
【题目】假设某种设备使用的年限x（年）与所支出的维修费用y（万元）有以下统计资料：
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2 | 4 | 5 | 6 | 7 |
若由资料知y对x呈线性相关关系。试求：
（1）求
； （2）线性回归方程
；
（3）估计使用10年时，维修费用是多少？
附：利用“最小二乘法”计算a,b的值时,可根据以下公式：
