题目内容
【题目】已知椭圆的长轴长为6,离心率为 ![]() ,F2为椭圆的右焦点.
,F2为椭圆的右焦点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)点M在圆x2+y2=8上,且M在第一象限,过M作圆x2+y2=8的切线交椭圆于P,Q两点,判断△PF2Q的周长是否为定值并说明理由.
【答案】解:(I)根据已知,设椭圆的标准方程为 ![]() , ∴2a=6,a=3,
, ∴2a=6,a=3, ![]() ,c=1;
,c=1;
b2=a2﹣c2=8,![]()
(II)△PF2Q的周长是定值,
设P(x1 , y1),Q(x2 , y2),则 ![]() ,
,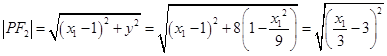 ,
,
∵0<x1<3,
∴ ![]() ,
,
在圆中,M是切点,
∴ 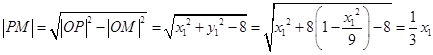 ,
,
∴ ![]() ,
,
同理|QF2|+|QM|=3,
∴|F2P|+|F2Q|+|PQ|=3+3=6,
因此△PF2Q的周长是定值6
【解析】(Ⅰ)由题意可知:2a=6, ![]() ,求得a和c的值,由b2=a2﹣c2 , 求得b,写出椭圆方程;(Ⅱ)设P(x1 , y1),Q(x2 , y2),分别求出|F2P|,|F2Q|,结合相切的条件可得|PM|2=|OP|2﹣|OM|2 , 可得
,求得a和c的值,由b2=a2﹣c2 , 求得b,写出椭圆方程;(Ⅱ)设P(x1 , y1),Q(x2 , y2),分别求出|F2P|,|F2Q|,结合相切的条件可得|PM|2=|OP|2﹣|OM|2 , 可得 ![]() ,同理|QF2|+|QM|=3,即可证明;
,同理|QF2|+|QM|=3,即可证明;

练习册系列答案
相关题目