题目内容
【题目】已知函数f(x)=ax2﹣(2a﹣1)x﹣lnx.
(1)当a>0时,求函数f(x)的单调递增区间;
(2)当a<0时,求函数f(x)在 ![]() 上的最小值;
上的最小值;
(3)记函数y=f(x)的图象为曲线C,设点A(x1 , y1),B(x2 , y2)是曲线C上的不同两点,点M为线段AB的中点,过点M作x轴的垂直交曲线C于点N,判断曲线C在点N处的切线是否平行于直线AB,并说明理由.
【答案】
(1)解:∵f(x)=ax2+(1﹣2a)x﹣lnx,
∴f′(x)=2ax+(1﹣2a)﹣ ![]() =
= ![]() ,
,
∵a>0,x>0,
∴2ax+1>0,解f′(x)>0,得x>1,
∴f(x)的单调增区间为(1,+∞)
(2)解:当a<0时,由f′(x)=0,得x1=﹣ ![]() ,x2=1,
,x2=1,
①当﹣ ![]() >1,即﹣
>1,即﹣ ![]() <a<0时,f(x)在(0,1)上是减函数,
<a<0时,f(x)在(0,1)上是减函数,
∴f(x)在[ ![]() ,1]上的最小值为f(1)=1﹣a.
,1]上的最小值为f(1)=1﹣a.
②当 ![]() ≤﹣
≤﹣ ![]() ≤1,即﹣1≤a≤﹣
≤1,即﹣1≤a≤﹣ ![]() 时,
时,
f(x)在[ ![]() ,﹣
,﹣ ![]() ]上是减函数,在[﹣
]上是减函数,在[﹣ ![]() ,1]上是增函数,
,1]上是增函数,
∴f(x)的最小值为f(﹣ ![]() )=1﹣
)=1﹣ ![]() +ln(﹣2a).
+ln(﹣2a).
③当﹣ ![]() <
< ![]() ,即a<﹣1时,f(x)在[
,即a<﹣1时,f(x)在[ ![]() ,1]上是增函数,
,1]上是增函数,
∴f(x)的最小值为f( ![]() )=
)= ![]() ﹣
﹣ ![]() a+ln2.
a+ln2.
综上,函数f(x)在区间[ ![]() ,1]上的最小值为:
,1]上的最小值为:
f(x)min= 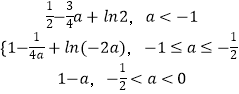 ;
;
(3)解:设M(x0,y0),则点N的横坐标为x0= ![]() ,
,
直线AB的斜率k1= ![]() =
= ![]() [a(x12﹣x22)+(1﹣2a)(x1﹣x2)+lnx2﹣lnx1]
[a(x12﹣x22)+(1﹣2a)(x1﹣x2)+lnx2﹣lnx1]
=a(x1+x2)+(1﹣2a)+ ![]() ,
,
曲线C在点N处的切线斜率k2=f′(x0)=2ax0+(1﹣2a)﹣ ![]() =a(x1+x2)+(1﹣2a)﹣
=a(x1+x2)+(1﹣2a)﹣ ![]() ,
,
假设曲线C在点N处的切线平行于直线AB,则k1=k2,
即 ![]() =﹣
=﹣ ![]() ,
,
∴ln ![]() =
= ![]() =
= ![]() ,
,
不妨设x1<x2, ![]() =t>1,则lnt=
=t>1,则lnt= ![]() ,
,
令g(t)=lnt﹣ ![]() (t>1),则g′(t)=
(t>1),则g′(t)= ![]() ﹣
﹣ ![]() =
= ![]() >0,
>0,
∴g(t)在(1,+∞)上是增函数,又g(1)=0,
∴g(t)>0,即lnt= ![]() 不成立,
不成立,
∴曲线C在点N处的切线不平行于直线AB
【解析】(1)求出函数f(x)的导函数,由a>0,定义域为(0,+∞),再由f′(x)>0求得函数f(x)的单调增区间;(2)当a<0时,求出导函数的零点﹣ ![]() ,1,分﹣
,1,分﹣ ![]() >1,
>1, ![]() ≤﹣
≤﹣ ![]() ≤1,﹣
≤1,﹣ ![]() <
< ![]() ,讨论函数f(x)在区间[
,讨论函数f(x)在区间[ ![]() ,1]上的单调性,求出函数的最小值,最后表示为关于a的分段函数;(3)设出线段AB的中点M的坐标,得到N的坐标,由两点式求出AB的斜率,再由导数得到曲线C过N点的切线的斜率,由斜率相等得到ln
,1]上的单调性,求出函数的最小值,最后表示为关于a的分段函数;(3)设出线段AB的中点M的坐标,得到N的坐标,由两点式求出AB的斜率,再由导数得到曲线C过N点的切线的斜率,由斜率相等得到ln ![]() =
= ![]() ,令
,令 ![]() =t后构造函数g(t)=lnt﹣
=t后构造函数g(t)=lnt﹣ ![]() (t>1),根据函数的单调性判断不成立.
(t>1),根据函数的单调性判断不成立.
【考点精析】掌握利用导数研究函数的单调性和函数的最大(小)值与导数是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案【题目】(本题满分12分)全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标.根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.
组号 | 分组 | 频数 |
1 |
| 2 |
2 |
| 8 |
3 |
| 7 |
4 |
| 3 |
(Ⅰ)现从融合指数在![]() 和
和![]() 内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在
内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在![]() 的概率;
的概率;
(Ⅱ)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.

