题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,且2cos2 cos B-sin(A-B)sin B+cos(A+C)=-
cos B-sin(A-B)sin B+cos(A+C)=- .
.
(1)求cos A的值;
(2)若a=4 ,b=5,求向量
,b=5,求向量 在
在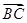 方向上的投影.
方向上的投影.
 cos B-sin(A-B)sin B+cos(A+C)=-
cos B-sin(A-B)sin B+cos(A+C)=- .
.(1)求cos A的值;
(2)若a=4
 ,b=5,求向量
,b=5,求向量 在
在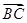 方向上的投影.
方向上的投影.(1)- (2)
(2)
 (2)
(2)
(1)由2cos2 cos B-sin(A-B)sin B+cos(A+C)=-
cos B-sin(A-B)sin B+cos(A+C)=- ,得
,得
[cos(A-B)+1]cos B-sin(A-B)sin B-cos B=- ,
,
∴cos(A-B)cos B-sin(A-B)sin B=- .
.
则cos(A-B+B)=- ,即cos A=-
,即cos A=- .
.
(2)由cos A=- ,0<A<π,得sin A=
,0<A<π,得sin A= ,
,
由正弦定理,有 ,所以,sin B=
,所以,sin B=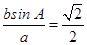 .
.
由题知a>b,则A>B,故B=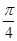 ,
,
根据余弦定理,有(4 )2=52+c2-2×5c×
)2=52+c2-2×5c×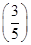 ,
,
解得c=1或c=-7(舍去).
故向量 在
在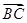 方向上的投影为|
方向上的投影为| |cos B=
|cos B= .
.
 cos B-sin(A-B)sin B+cos(A+C)=-
cos B-sin(A-B)sin B+cos(A+C)=- ,得
,得[cos(A-B)+1]cos B-sin(A-B)sin B-cos B=-
 ,
,∴cos(A-B)cos B-sin(A-B)sin B=-
 .
.则cos(A-B+B)=-
 ,即cos A=-
,即cos A=- .
.(2)由cos A=-
 ,0<A<π,得sin A=
,0<A<π,得sin A= ,
,由正弦定理,有
 ,所以,sin B=
,所以,sin B=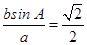 .
.由题知a>b,则A>B,故B=
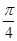 ,
,根据余弦定理,有(4
 )2=52+c2-2×5c×
)2=52+c2-2×5c×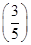 ,
,解得c=1或c=-7(舍去).
故向量
 在
在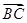 方向上的投影为|
方向上的投影为| |cos B=
|cos B= .
.
练习册系列答案
相关题目
 中,角
中,角 的对边分别为
的对边分别为 ,已知
,已知 ,
,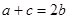 ;
; ,求
,求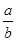 的值.
的值.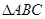 中,角
中,角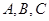 的对边分别为
的对边分别为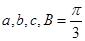 ,
,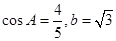 。
。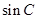 的值;
的值;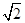 (B)2
(B)2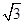 (C)
(C)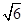 -
-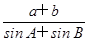 的值;
的值;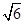 ,∠B=2∠A.
,∠B=2∠A.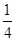 ,b=2,sin C=2sin A,则△ABC的面积为( ).
,b=2,sin C=2sin A,则△ABC的面积为( ).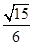
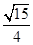
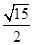
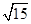
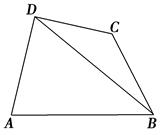
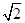
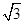
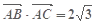 ,
,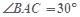 ,若△MBC, △MCA和△MAB的面积分别
,若△MBC, △MCA和△MAB的面积分别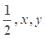 ,则
,则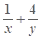 的最小值是 ( )
的最小值是 ( )