题目内容
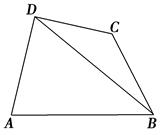
如图,在四边形ABCD中,已知AD⊥CD,AD=10,AB=14,∠BDA=60°,∠BCD=135°,则BC的长为 ( ).

A.8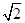 | B.9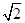 |
C.14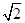 | D.8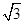 |
A
在△ABD中,设BD=x,则BA2=BD2+AD2-2BD·AD·cos∠BDA,
即142=x2+102-2·10x·cos 60°,
整理得x2-10x-96=0,
解得x1=16,x2=-6(舍去).
由正弦定理得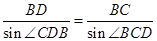 ,∴BC=
,∴BC=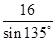 ·sin 30°=8
·sin 30°=8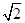 .
.
即142=x2+102-2·10x·cos 60°,
整理得x2-10x-96=0,
解得x1=16,x2=-6(舍去).
由正弦定理得
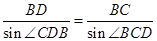 ,∴BC=
,∴BC=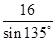 ·sin 30°=8
·sin 30°=8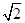 .
.
练习册系列答案
相关题目
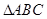 中,角
中,角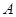 ,
,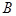 ,
,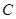 对应的边分别是
对应的边分别是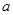 ,
,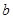 ,
,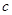 .已知
.已知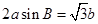 .
.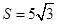 ,
,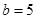 ,求
,求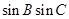 的值.
的值.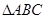 中,内角
中,内角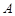 ,
,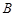 ,
,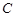 的对边分别为
的对边分别为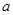 ,
,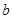 ,
,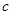 ,且
,且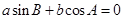 .
.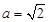 ,
,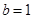 ,求
,求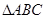 中,角
中,角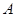 ,
,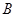 ,
,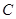 的对边为
的对边为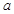 ,
,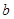 ,
,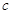 且;
且;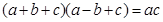
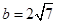 ,
,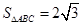 ,求
,求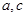 的值.
的值.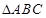 中,
中,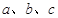 分别为角
分别为角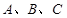 的对边,△ABC的面积S满足
的对边,△ABC的面积S满足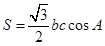 .
.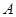 的值;
的值;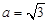 ,设角
,设角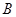 的大小为
的大小为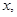 用
用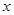 表示
表示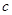 ,并求
,并求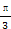 <C<
<C<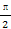 且
且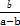 =
=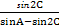 .
.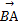 +
+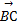 |=2,求
|=2,求 cos B-sin(A-B)sin B+cos(A+C)=-
cos B-sin(A-B)sin B+cos(A+C)=- .
. ,b=5,求向量
,b=5,求向量 在
在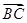 方向上的投影.
方向上的投影.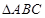 的内角
的内角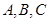 所对边的长分别为
所对边的长分别为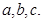 若
若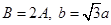 ,则角
,则角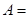 ( )
( )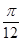
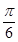
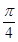
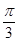
 ,cos B=
,cos B=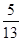 ,b=3,则c=________.
,b=3,则c=________.