题目内容
【题目】从一张半径为3的圆形铁皮中裁剪出一块扇形铁皮（如图1阴影部分），并卷成一个深度为
米的圆锥筒（如图2）.若所裁剪的扇形铁皮的圆心角为
.
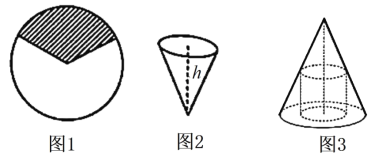
（1）求圆锥筒的容积；
（2）在（1）中的圆锥内有一个底面圆半径为
的内接圆柱（如图3），求内接圆柱侧面积最大时的值.
【答案】（1）
；（2）
.
【解析】
（1）根据圆锥的结构特征，扇形即为为圆锥的侧面展开图，求出圆锥的底面半径和高，即可求出容积；
（2）根据圆柱内接圆锥关系，求出圆柱的高与底面半径
的关系式，进而求出圆柱侧面积的目标函数，根据函数特征求其最值即可.
（1）设圆锥筒的半径为
，容积为
，
∵所裁剪的扇形铁皮的圆心角为
，
∴
，解得
，
∴
，
∴
.
∴圆锥筒的容积为.
（2）设内接圆柱高为
则有，由圆锥内接圆柱的轴截面图，
得
，
所以内接圆柱侧面积
，
所以当
时内接圆柱侧面积最大.
练习册系列答案
相关题目
