题目内容
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 是参数),
是参数),
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,曲线
,曲线![]() 任一点为
任一点为![]() ,求点
,求点![]() 直线
直线![]() 的距离的最大值.
的距离的最大值.
【答案】(Ⅰ)直线![]() 的普通方程为
的普通方程为![]() ,曲线
,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(1)利用代入消参法得到直线![]() 的普通方程,利用
的普通方程,利用![]() 得到曲线
得到曲线![]() 的直角坐标方程;(2)曲线
的直角坐标方程;(2)曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() 为
为![]() ,利用点到直线距离公式得到点
,利用点到直线距离公式得到点![]() 直线
直线![]() 的距离,进而求出最大值.
的距离,进而求出最大值.
试题解析:
(Ⅰ)直线![]() 的普通方程为
的普通方程为![]() ,
,
∵![]() ∴
∴![]() ∴
∴![]()
故曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
(Ⅱ)由(Ⅰ)得![]() ,经过伸缩变换
,经过伸缩变换![]() 得到曲线
得到曲线![]() 的方程为
的方程为![]() ,所以曲线
,所以曲线![]() 的方程
的方程![]() ,可以令
,可以令![]() (
(![]() 是参数),根据点到直线的距离公式可得
是参数),根据点到直线的距离公式可得![]()
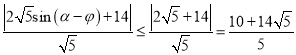 ,
,
故点![]() 到直线
到直线![]() 的距离的最大值为
的距离的最大值为![]() .
.

练习册系列答案
相关题目
【题目】(本题14分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(![]() 吨)与相应的生产能耗
吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |

(1)请画出上表数据的散点图;并指出x,y 是否线性相关;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式 ,
,![]() )
)