题目内容
如图,在三棱锥P—ABC中,∠APB=∠BPC=∠APC=90°,M在△ABC内,∠MPA=60°,∠MPB=45°,则∠MPC的度数为( )
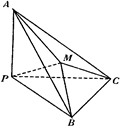
| A.30° | B.45° | C. 75° | D.60° |

D
分析:过M做平面PBC的垂线,交平面PBC于Q,连接PQ,由公式:cos∠MPB=cos∠MPQ×cos∠QPB,得到cos∠QPB=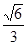 ,从而可得cos∠QPC=
,从而可得cos∠QPC= 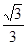 ,再用公式:cos∠MPC=cos∠MPQ×cos∠QPC,即可求∠MPC.
,再用公式:cos∠MPC=cos∠MPQ×cos∠QPC,即可求∠MPC.
解答:解:过M做平面PBC的垂线,交平面PBC于Q,连接PQ.
∵∠APB=∠APC=90°,∴AP⊥平面PBC,
∵MQ⊥平面PBC,∴AP∥MQ
∵∠MPA=60°,∴∠MPQ=90°-60°=30°.
由公式:cos∠MPB=cos∠MPQ×cos∠QPB,得到cos∠QPB=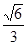
∵∠QPC是∠QPB的余角,所以cos∠QPC=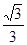
再用公式:cos∠MPC=cos∠MPQ×cos∠QPC,得到cos∠MPC=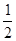
∴∠MPC=60°
故选C.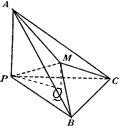
点评:本题考查空间角,考查学生分析解决问题的能力,利用好公式是关键.
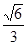 ,从而可得cos∠QPC=
,从而可得cos∠QPC= 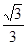 ,再用公式:cos∠MPC=cos∠MPQ×cos∠QPC,即可求∠MPC.
,再用公式:cos∠MPC=cos∠MPQ×cos∠QPC,即可求∠MPC.解答:解:过M做平面PBC的垂线,交平面PBC于Q,连接PQ.
∵∠APB=∠APC=90°,∴AP⊥平面PBC,
∵MQ⊥平面PBC,∴AP∥MQ
∵∠MPA=60°,∴∠MPQ=90°-60°=30°.
由公式:cos∠MPB=cos∠MPQ×cos∠QPB,得到cos∠QPB=
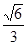
∵∠QPC是∠QPB的余角,所以cos∠QPC=
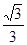
再用公式:cos∠MPC=cos∠MPQ×cos∠QPC,得到cos∠MPC=
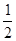
∴∠MPC=60°
故选C.

点评:本题考查空间角,考查学生分析解决问题的能力,利用好公式是关键.

练习册系列答案
相关题目
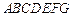 中,
中,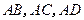 两两垂直,平面
两两垂直,平面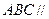 平面
平面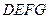 ,
,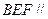 平面
平面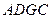 ,
,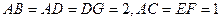 .
.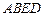 是正方形;
是正方形;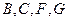 是否四点共面,并说明为什么?
是否四点共面,并说明为什么?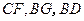 ,求证:
,求证: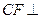 平面
平面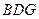 .
.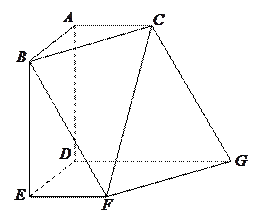
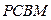 ⊥平面
⊥平面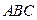 ,
,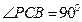 ,
,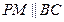 ,
,
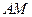 与直线
与直线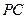 所成的角为
所成的角为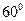 ,又
,又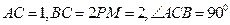 。
。 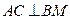 ;
;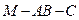 的余弦值
的余弦值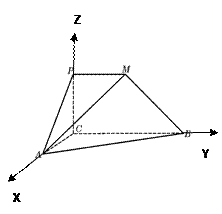
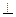 平面ABC,BD//AE,且AC=AB=BC=AE=1,BD=2,F为CD中点。
平面ABC,BD//AE,且AC=AB=BC=AE=1,BD=2,F为CD中点。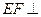 平面BCD;
平面BCD;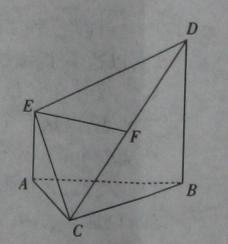
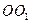 内有一个三棱柱
内有一个三棱柱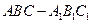 ,三棱柱的 底面为圆柱
,三棱柱的 底面为圆柱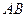 是圆
是圆 的直径。
的直径。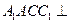 平面
平面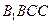 ;
;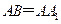 ,在圆
,在圆 柱
柱 。
。 在圆周上运动时,求
在圆周上运动时,求 与平面
与平面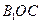 所成的角为
所成的角为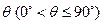 。当
。当
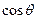 的值。
的值。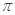
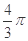
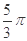



 ∠AEF=45°
∠AEF=45°
