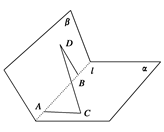
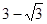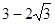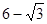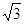题目内容
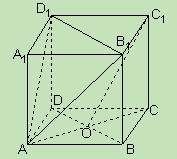
(14分)如图,圆柱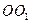 内有一个三棱柱
内有一个三棱柱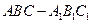 ,三棱柱的 底面为圆柱
,三棱柱的 底面为圆柱
底面的内接三角形,且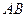 是圆
是圆 的直径。
的直径。
(I)证明:平面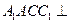 平面
平面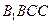 ;
;
(II)设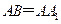 ,在圆
,在圆 柱
柱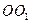 内随机选取一点,记该点取自三棱柱
内随机选取一点,记该点取自三棱柱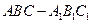 内的概率为
内的概率为 。
。
(i)当点 在圆周上运动时,求
在圆周上运动时,求 的最大值;
的最大值;
(ii)如果平面 与平面
与平面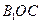 所成的角为
所成的角为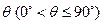 。当
。当 取最大值时,求
取最大值时,求
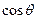 的值。
的值。
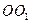 内有一个三棱柱
内有一个三棱柱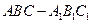 ,三棱柱的 底面为圆柱
,三棱柱的 底面为圆柱底面的内接三角形,且
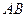 是圆
是圆 的直径。
的直径。(I)证明:平面
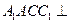 平面
平面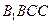 ;
;(II)设
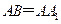 ,在圆
,在圆 柱
柱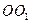 内随机选取一点,记该点取自三棱柱
内随机选取一点,记该点取自三棱柱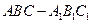 内的概率为
内的概率为 。
。(i)当点
 在圆周上运动时,求
在圆周上运动时,求 的最大值;
的最大值;(ii)如果平面
 与平面
与平面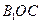 所成的角为
所成的角为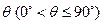 。当
。当 取最大值时,求
取最大值时,求
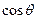 的值。
的值。解:(Ⅰ)因为
 平面ABC,
平面ABC, 平面ABC,所以
平面ABC,所以

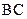 ,
,
因为AB是圆O直径,所以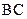

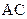 ,又
,又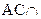
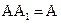 ,所以
,所以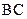
 平面
平面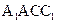 ,
,
而 平面
平面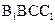 ,所以平面
,所以平面 平面
平面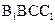 。
。
(Ⅱ)(i)设圆柱的底面半径为 ,则AB=
,则AB= ,故三棱柱
,故三棱柱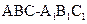 的体积为
的体积为
 =
= ,
,
又因为 ,
,
所以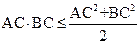 =
=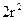 ,当且仅当
,当且仅当 时等号成立,
时等号成立,
从而 ,而圆柱的体积
,而圆柱的体积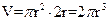 ,
,
故 =
=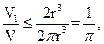 当且仅当
当且仅当 ,即
,即 时等号成立,
时等号成立,
所以 的最大值是
的最大值是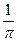 。
。
(ii)由(i)可知, 取最大值时,
取最大值时, ,于是以O为坐标原点,建立空间直角坐标系
,于是以O为坐标原点,建立空间直角坐标系 (如图),则C(r,0,0),B(0,r,0),
(如图),则C(r,0,0),B(0,r,0),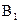 (
( 0,r,2r),
0,r,2r),
因为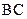
 平面
平面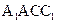 ,所以
,所以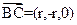 是平面
是平面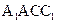 的一个法向量,
的一个法向量,
设平面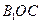 的法向量
的法向量 ,
,
由 ,故
,故 ,
,
取 得平面
得平面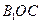 的一个法向量为
的一个法向量为 ,因为
,因为 ,
,
所以 。
。

 平面ABC,
平面ABC, 平面ABC,所以
平面ABC,所以

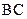 ,
,因为AB是圆O直径,所以
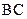

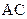 ,又
,又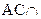
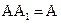 ,所以
,所以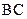
 平面
平面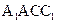 ,
,而
 平面
平面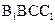 ,所以平面
,所以平面 平面
平面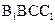 。
。(Ⅱ)(i)设圆柱的底面半径为
 ,则AB=
,则AB= ,故三棱柱
,故三棱柱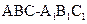 的体积为
的体积为 =
= ,
,又因为
 ,
,所以
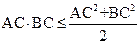 =
=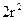 ,当且仅当
,当且仅当 时等号成立,
时等号成立,从而
 ,而圆柱的体积
,而圆柱的体积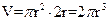 ,
,故
 =
=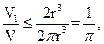 当且仅当
当且仅当 ,即
,即 时等号成立,
时等号成立,所以
 的最大值是
的最大值是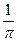 。
。(ii)由(i)可知,
 取最大值时,
取最大值时, ,于是以O为坐标原点,建立空间直角坐标系
,于是以O为坐标原点,建立空间直角坐标系 (如图),则C(r,0,0),B(0,r,0),
(如图),则C(r,0,0),B(0,r,0),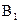 (
( 0,r,2r),
0,r,2r),因为
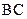
 平面
平面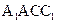 ,所以
,所以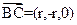 是平面
是平面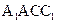 的一个法向量,
的一个法向量,设平面
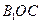 的法向量
的法向量 ,
,由
 ,故
,故 ,
,取
 得平面
得平面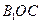 的一个法向量为
的一个法向量为 ,因为
,因为 ,
,所以
 。
。略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
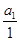 =
=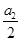 =
=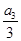 =k,则
=k,则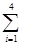 (ihi)=
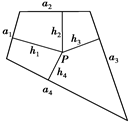
(ihi)=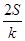 .类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为hi(i=1,2,3,4),若
.类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为hi(i=1,2,3,4),若
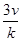
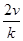
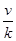
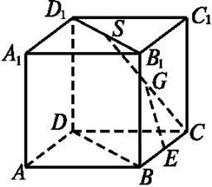
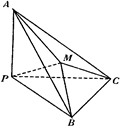
 本小题满分12分)如图,在三棱柱
本小题满分12分)如图,在三棱柱 中,
中, 面
面 ,
,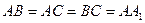 ,
,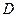 ,
,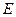 分别为
分别为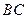 ,
,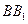
 的中点.
的中点.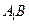 ∥平面
∥平面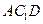 ; (2)求证:
; (2)求证: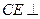 平面
平面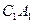 与平面
与平面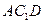 所成的角的
所成的角的 正弦值.
正弦值.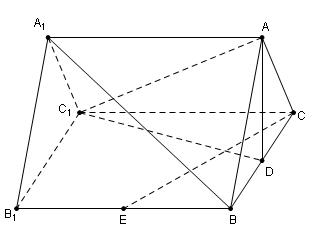
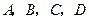 为空间四点.在
为空间四点.在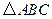 中,
中,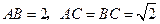 .等
.等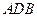 以
以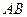 为轴运动.
为轴运动.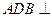 平面
平面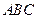 时,求
时,求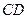 ;
; 转动时,是否总有
转动时,是否总有 ?证明你的结论.
?证明你的结论.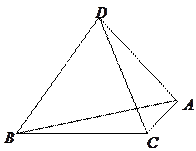
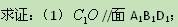
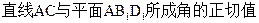
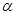 ,
,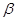 ,
,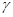 两两互相垂直,点
两两互相垂直,点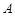 ∈
∈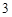 ,点
,点 是
是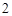 倍,则点
倍,则点