题目内容
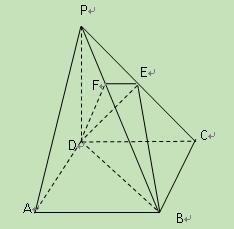
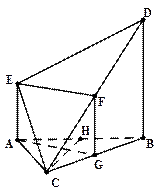
(本小题满分12分)如图,在多面体ABDEC中,AE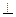 平面ABC,BD//AE,且AC=AB=BC=AE=1,BD=2,F为CD中点。
平面ABC,BD//AE,且AC=AB=BC=AE=1,BD=2,F为CD中点。
(I)求证:EF//平面ABC;
(II)求证: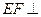 平面BCD;
平面BCD;
(III)求多面体ABDEC的体积。
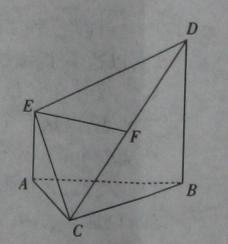
 平面ABC,BD//AE,且AC=AB=BC=AE=1,BD=2,F为CD中点。
平面ABC,BD//AE,且AC=AB=BC=AE=1,BD=2,F为CD中点。(I)求证:EF//平面ABC;
(II)求证:
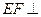 平面BCD;
平面BCD;(III)求多面体ABDEC的体积。

(1)找BC中点G点,连接AG,FG
 F,G分别为DC,BC中点
F,G分别为DC,BC中点
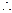

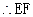 //AG
//AG
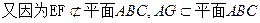
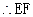 //平面ABC ……….4分
//平面ABC ……….4分
(2)因为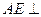 面
面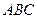 ,
,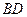 ∥
∥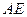
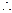 DB⊥平面ABC
DB⊥平面ABC
又∵DB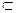 平面
平面
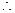 平面ABC⊥平面
平面ABC⊥平面
又∵G为 BC中点且AC=AB=BC
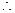 AG⊥BC
AG⊥BC
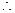 AG⊥平面
AG⊥平面 ,
,
又∵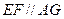
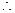
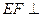 平面
平面 ……………………….8分
……………………….8分
(3)过C作CH⊥AB,则CH⊥平面ABDE且CH=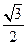
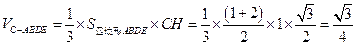 …………12分
…………12分

 F,G分别为DC,BC中点
F,G分别为DC,BC中点

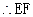 //AG
//AG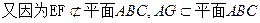
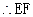 //平面ABC ……….4分
//平面ABC ……….4分(2)因为
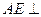 面
面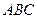 ,
,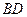 ∥
∥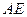
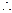 DB⊥平面ABC
DB⊥平面ABC又∵DB
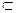 平面
平面
 平面ABC⊥平面
平面ABC⊥平面
又∵G为 BC中点且AC=AB=BC
 AG⊥BC
AG⊥BC AG⊥平面
AG⊥平面 ,
,又∵
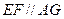
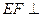 平面
平面 ……………………….8分
……………………….8分(3)过C作CH⊥AB,则CH⊥平面ABDE且CH=
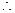
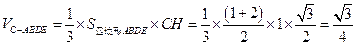 …………12分
…………12分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
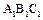 中,
中, ,D,E分别为BC,
,D,E分别为BC,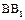 的中点,
的中点,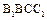 是边长为6的正方形.
是边长为6的正方形.
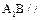 平面
平面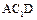 ;
;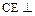 平面
平面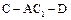 的余弦值.
的余弦值.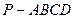 中,底面
中,底面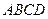 是矩形,
是矩形,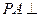 平面
平面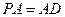 ,点
,点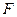 是棱
是棱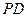 的中点,点
的中点,点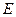 在棱
在棱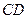 上移动.
上移动.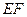 与平面
与平面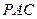 的关系,并说明理由;
的关系,并说明理由;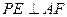 .
.
 BC,CD,DB分别将△BCA2,△CDA3,△DBA1翻折上去恰好使A1,A2,A3重合于一点A。
BC,CD,DB分别将△BCA2,△CDA3,△DBA1翻折上去恰好使A1,A2,A3重合于一点A。
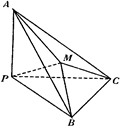
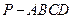 中,底面
中,底面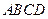 是正方形,侧棱
是正方形,侧棱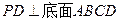 ,
,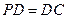 ,
,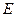 是
是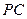 的中点,作
的中点,作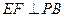 交
交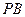 于点
于点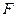 .
.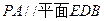 ;
;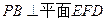 .
.