题目内容
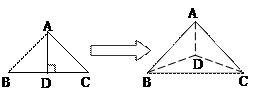
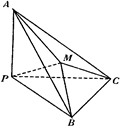
18.(本小题满分13分)如图,平面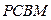 ⊥平面
⊥平面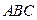 ,
,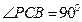 ,
,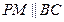 ,
,
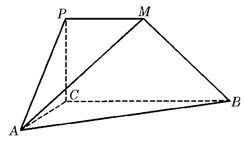
直线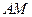 与直线
与直线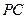 所成的角为
所成的角为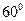 ,又
,又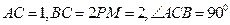 。
。
(1)求证: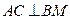 ;
;
(2)求二面角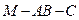 的余弦值
的余弦值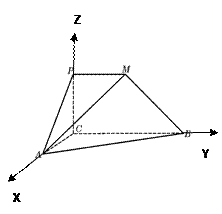
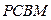 ⊥平面
⊥平面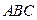 ,
,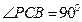 ,
,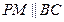 ,
,
直线
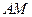 与直线
与直线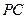 所成的角为
所成的角为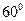 ,又
,又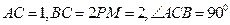 。
。 (1)求证:
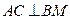 ;
;(2)求二面角
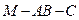 的余弦值
的余弦值
 解:
解: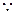 面
面
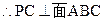 ┅┅┅┅2分
┅┅┅┅2分如图以
 为原点建立空间直角坐标系
为原点建立空间直角坐标系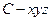 .
. 设
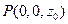
 则
则 ,
,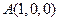 ,
,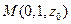 .
. 
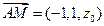 ,
,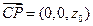
由直线
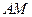 与直线
与直线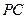 所成的角为60°,得
所成的角为60°,得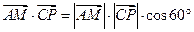 ,即
,即 ,解得
,解得 .┅┅┅4分
.┅┅┅4分(1)∴
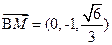 ,
, ,得
,得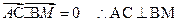 ┅┅┅6分
┅┅┅6分∴
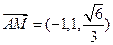 ,
,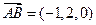 ┅┅┅8分
┅┅┅8分(2)设平面
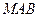 的一个法向量为
的一个法向量为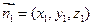 ,则
,则由
 ,取
,取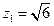 ,得
,得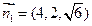 ┅┅┅┅10分
┅┅┅┅10分取平面
 的一个法向量为
的一个法向量为
则
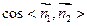
 ┅┅┅┅12分
┅┅┅┅12分由图知二面角
 的大小的余弦值为
的大小的余弦值为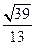 ┅┅┅┅13分
┅┅┅┅13分方法二:(1)因为
 ┅┅┅3分
┅┅┅3分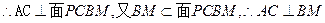 ┅┅┅6分
┅┅┅6分(2)同上
略

练习册系列答案
相关题目
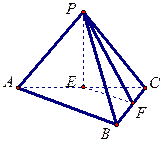
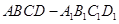 中,点P是面
中,点P是面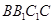 内一动点,若点P到直线BC与直线
内一动点,若点P到直线BC与直线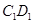 的距离相等,则动点P的轨迹所在的曲线是 ( )
的距离相等,则动点P的轨迹所在的曲线是 ( )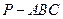 中,
中,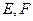 分别为
分别为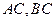 的中点。
的中点。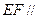 平面
平面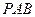 ;
;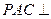 平面
平面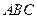 ,且
,且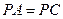 ,
,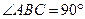 ,求证:平面
,求证:平面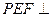 平面
平面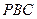 。
。
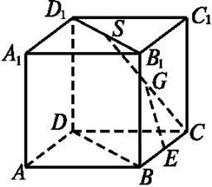
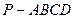 中,底面
中,底面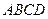 是矩形,
是矩形,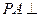 平面
平面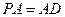 ,点
,点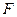 是棱
是棱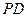 的中点,点
的中点,点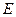 在棱
在棱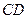 上移动.
上移动.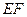 与平面
与平面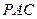 的关系,并说明理由;
的关系,并说明理由;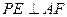 .
.
 截一球面得圆
截一球面得圆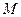 ,过圆心
,过圆心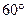 二面角的平面
二面角的平面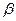 截该球面得圆
截该球面得圆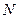 ,若该球面的半径为4,圆
,若该球面的半径为4,圆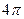 ,则圆
,则圆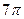 (B)
(B)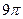 (c)
(c)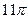 (D)
(D)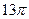
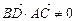 ;
;