题目内容
设、是两条不同的直线,、是两个不同的平面,给出下列5个命题:
①若,,则 ;
②若,,,则;
③若 ,,,则;
④若 ,,,则;
⑤若,,,则.
其中正确命题的个数是
①若,,则 ;
②若,,,则;
③若 ,,,则;
④若 ,,,则;
⑤若,,,则.
其中正确命题的个数是
| A.1 | B.2 | C.3 | D.4 |
B
根据空间面面垂直、平行的判定和性质,以及线面垂直、平行的判定与性质可以证出②③是真命题,而且①④⑤缺少条件,是假命题.由此可得本题的答案.
解:对于①,m⊥α,l⊥β,没有指出平面α、β的位置关系,也没有指出m、l的位置关系,
因此不能确定l与α的位置关系,故①不正确;
对于②,由m⊥α,l∥m,得l⊥α,再结合l?β,可得α⊥β,故②正确;
对于③,由α∥β,l⊥α,得l⊥β,结合m∥β,可得l⊥m,故③正确;
对于④,由α∥β,l∥α,得l∥β或l?β,结合m?β,得l与m平行、相交或异面都有可能,故④不正确;
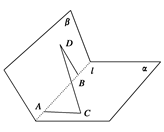
对于⑤,若α⊥β,α∩β=l,m⊥l,当m是α内的直线时有m⊥β,但条件中没有“m?α”这一条,
不一定有m⊥β,故⑤不正确.
因此正确命题为②③,共2个
故选B

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
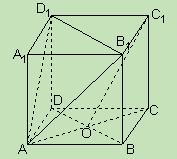
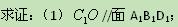

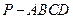 中,底面
中,底面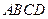 是正方形,侧棱
是正方形,侧棱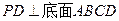 ,
,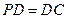 ,
, 是
是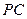 的中点,作
的中点,作 交
交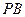 于点
于点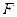 .
.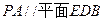 ;
;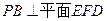 .
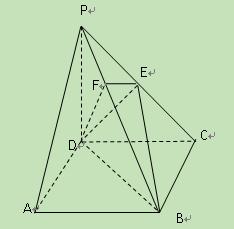
.
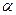
 截一球面得圆
截一球面得圆 ,过圆心
,过圆心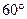 二面角的平面
二面角的平面 截该球面得圆
截该球面得圆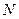 ,若该球面的半径为4,圆
,若该球面的半径为4,圆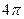 ,则圆
,则圆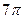 (B)
(B) (c)
(c)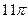 (D)
(D)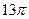
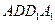 和
和 三棱锥
三棱锥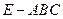 组合而成,点
组合而成,点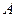 、
、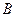 、
、 在圆
在圆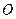 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图所示,其中 ,
,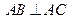 ,
,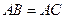 ,
, .
.
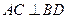 ;
;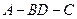 的平面角的大小.
的平面角的大小. 的底面为直角梯形,
的底面为直角梯形,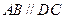 ,
,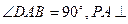 底面
底面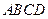 ,且
,且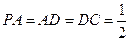 ,
,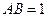 ,
,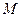 是
是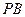 的中点。
的中点。 面
面 ;
;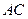 与
与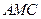 与面
与面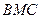 所成二面角的余弦值.
所成二面角的余弦值.
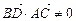 ;
;