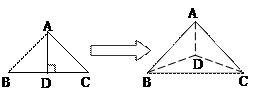
题目内容
(本小题满分16分)
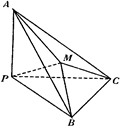
如图,多面体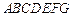 中,
中,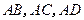 两两垂直,平面
两两垂直,平面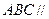 平面
平面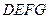 ,
,
平面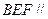 平面
平面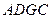 ,
,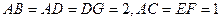 .
.
(1)证明四边形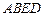 是正方形;
是正方形;
(2)判断点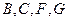 是否四点共面,并说明为什么?
是否四点共面,并说明为什么?
(3)连结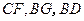 ,求证:
,求证: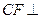 平面
平面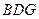 .
.
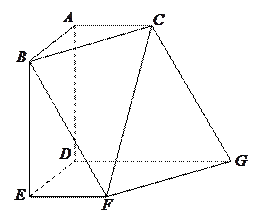
如图,多面体
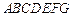 中,
中,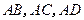 两两垂直,平面
两两垂直,平面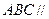 平面
平面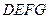 ,
,平面
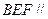 平面
平面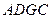 ,
,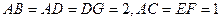 .
.(1)证明四边形
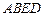 是正方形;
是正方形;(2)判断点
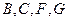 是否四点共面,并说明为什么?
是否四点共面,并说明为什么?(3)连结
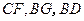 ,求证:
,求证: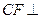 平面
平面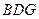 .
.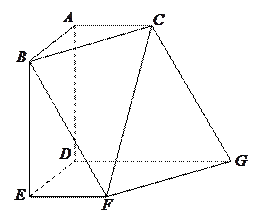
证明:(1)
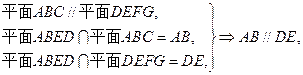
…………..2分
同理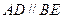 ,……..3分
,……..3分
则四边形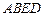 是平行四边形.
是平行四边形.
又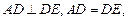
 四边形
四边形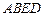 是正方形. ……..4分
是正方形. ……..4分
(2) 取 中点
中点 ,连接
,连接 .
.
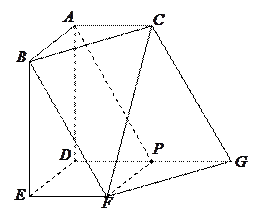
在梯形 中,
中, 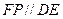 且
且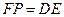 .
.
又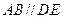 且
且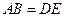 ,
,

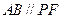 且
且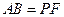 .……………………..5分
.……………………..5分
 四边形
四边形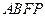 为平行四边形, ……………………..6分
为平行四边形, ……………………..6分

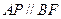 . ……………………..7分
. ……………………..7分
在梯形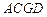 中,
中,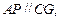

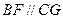 , ……………………..9分
, ……………………..9分

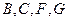 四点共面. …………………….10分
四点共面. …………………….10分
(3)同(1)中证明方法知四边形BFGC为平行四边形.
且有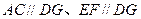 ,从而
,从而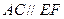 ,
,
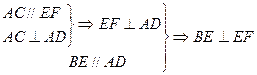 . ……………………..12分
. ……………………..12分
又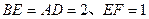 故
故 ,而
,而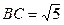 ,
,
故四边形BFGC为菱形,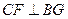 . ……………………..14分
. ……………………..14分
又由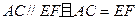 知
知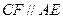 .
.
正方形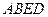 中,
中,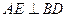 ,故
,故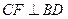 .
.
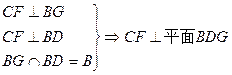 . ……………………..16分
. ……………………..16分
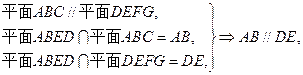
…………..2分
同理
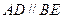 ,……..3分
,……..3分则四边形
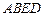 是平行四边形.
是平行四边形.又
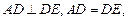
 四边形
四边形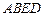 是正方形. ……..4分
是正方形. ……..4分(2) 取
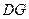 中点
中点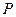 ,连接
,连接 .
.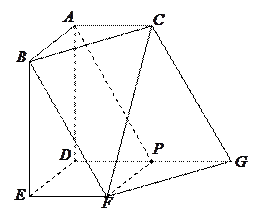
在梯形
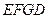 中,
中, 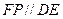 且
且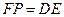 .
.又
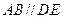 且
且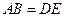 ,
,
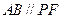 且
且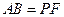 .……………………..5分
.……………………..5分 四边形
四边形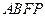 为平行四边形, ……………………..6分
为平行四边形, ……………………..6分
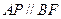 . ……………………..7分
. ……………………..7分在梯形
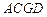 中,
中,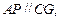

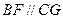 , ……………………..9分
, ……………………..9分
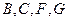 四点共面. …………………….10分
四点共面. …………………….10分(3)同(1)中证明方法知四边形BFGC为平行四边形.
且有
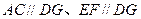 ,从而
,从而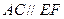 ,
,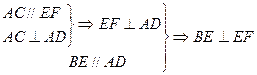 . ……………………..12分
. ……………………..12分又
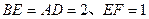 故
故 ,而
,而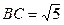 ,
,故四边形BFGC为菱形,
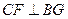 . ……………………..14分
. ……………………..14分又由
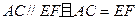 知
知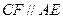 .
.正方形
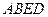 中,
中,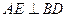 ,故
,故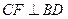 .
.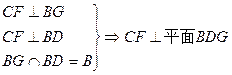 . ……………………..16分
. ……………………..16分略

练习册系列答案
相关题目
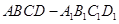 中,点P是面
中,点P是面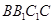 内一动点,若点P到直线BC与直线
内一动点,若点P到直线BC与直线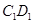 的距离相等,则动点P的轨迹所在的曲线是 ( )
的距离相等,则动点P的轨迹所在的曲线是 ( )
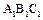 中,
中, ,D,E分别为BC,
,D,E分别为BC,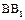 的中点,
的中点,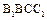 是边长为6的正方形.
是边长为6的正方形.
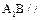 平面
平面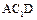 ;
;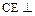 平面
平面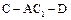 的余弦值.
的余弦值.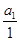 =
=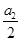 =
=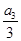 =k,则
=k,则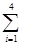 (ihi)=
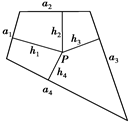
(ihi)=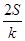 .类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为hi(i=1,2,3,4),若
.类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为hi(i=1,2,3,4),若
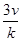
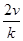
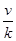
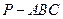 中,
中,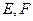 分别为
分别为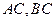 的中点。
的中点。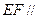 平面
平面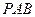 ;
;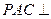 平面
平面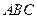 ,且
,且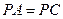 ,
,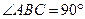 ,求证:平面
,求证:平面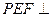 平面
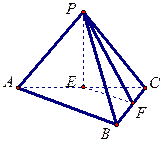
平面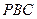 。
。
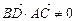 ;
;