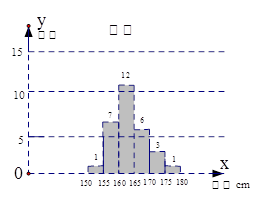
题目内容
已知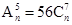 ,且(1-2x)n=a0+a1x+a2x2+a3x3+……+anxn.
,且(1-2x)n=a0+a1x+a2x2+a3x3+……+anxn.
(Ⅰ)求n的值;
(Ⅱ)求a1+a2+a3+……+an的值。
(Ⅰ)15(Ⅱ)-2
解析试题分析:(Ⅰ)由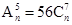 得:
得: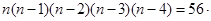
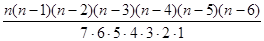
即(n-5)(n-6)=90
解之得:n=15或n=-4(舍去).
∴n=15.
(Ⅱ)当n=15时,由已知有:
(1-2x)15=a0+a1x+a2x2+a3x3+……+a15x15,
令x=1得:a0+a1+a2+a3+……+a15=-1,
令x=0得:a0=1,
∴a1+a2+a3+……+a15=-2.
考点:本小题主要考查排列数公式和组合数公式的应用以及二项展开式的系数的计算和应用.
点评:应用排列数公式和组合数公式时要准确及时,解决二项展开式的系数问题的主要方法是“赋值法”.

练习册系列答案
相关题目
 展开式中的所有二项式系数和为512,
展开式中的所有二项式系数和为512,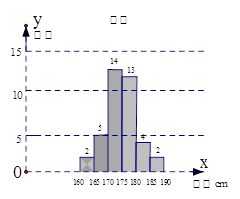
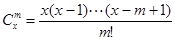 ,其中x∈R,m是正整数,且
,其中x∈R,m是正整数,且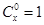 ,这是组合数
,这是组合数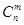 (n、m是正整数,且m≤n)的一种推广.
(n、m是正整数,且m≤n)的一种推广.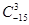 的值;
的值;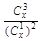 取得最小值?
取得最小值?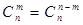 . ②
. ②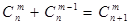 .
.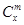 (x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
(x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由. 的展开式中,某一项的系数是它前一项系数的2倍,而又等于它后一项系数的
的展开式中,某一项的系数是它前一项系数的2倍,而又等于它后一项系数的
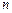 是给定的正整数,有序数组
是给定的正整数,有序数组 同时满足下列条件:
同时满足下列条件: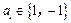 ,
,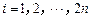 ; ②对任意的
; ②对任意的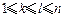 ,都有
,都有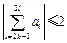 .
.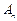 为满足“对任意的
为满足“对任意的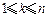 ,都有
,都有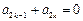 ”的有序数组
”的有序数组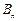 为满足“存在
为满足“存在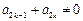 ”的有序数组
”的有序数组 的站法。
的站法。