题目内容
20.过点(3,-2)且与椭圆4x2+9y2=36有相同焦点的椭圆的方程是( )| A. | $\frac{{x}^{2}}{10}$+$\frac{{y}^{2}}{15}$=1 | B. | $\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{10}$=1 | C. | $\frac{{x}^{2}}{15}$+$\frac{{y}^{2}}{10}$=1 | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{10}$=1 |
分析 由已知椭圆的方程求出其半焦距,再设出待求椭圆方程,根据点(3,-2)在椭圆上结合隐含条件联立方程组求得答案.
解答 解:由椭圆4x2+9y2=36,得$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}=1$,
∴$c=\sqrt{9-4}=\sqrt{5}$,
设所求椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0).
则$\left\{\begin{array}{l}{\frac{9}{{a}^{2}}+\frac{4}{{b}^{2}}=1}\\{{a}^{2}={b}^{2}+5}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{a}^{2}=15}\\{{b}^{2}=10}\end{array}\right.$.
∴椭圆的方程是:$\frac{{x}^{2}}{15}+\frac{{y}^{2}}{10}=1$.
故选:C.
点评 本题考查椭圆方程的求法,考查方程组的解法,是基础题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
10.已知点P是边长为4的正方形内任一点,则点P到四个顶点的距离均大于2的概率是( )
| A. | $\frac{π}{4}$ | B. | 1-$\frac{π}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{π}{3}$ |
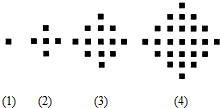 某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.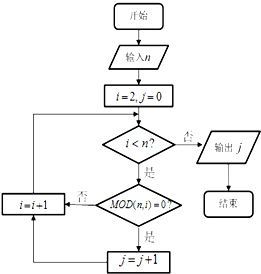 已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2.如图是一个算法的程序框图,当输入的值为36时,则输出的结果为( )
已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2.如图是一个算法的程序框图,当输入的值为36时,则输出的结果为( )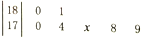 一次选拔运动员,测得7名选手的身高(单位:cm)分布茎叶图如图所示,已知记录的平均身高为177cm,有1名选手的身高记录不清楚,其末位数记为x,那么x的值为( )
一次选拔运动员,测得7名选手的身高(单位:cm)分布茎叶图如图所示,已知记录的平均身高为177cm,有1名选手的身高记录不清楚,其末位数记为x,那么x的值为( )