Question

【题目】如图，正四棱锥S－ABCD中，SA＝AB＝2，E，F，G分别为BC，SC，CD的中点．设P为线段FG上任意一点．

(1)求证：EP⊥AC；

(2)当P为线段FG的中点时，求直线BP与平面EFG所成角的余弦值．

Answer 1

【答案】(1)见解析；(2)

【解析】试题分析：（1）先证AC⊥平面SBD，再证平面EFG∥平面BSD，即得AC⊥平面GEF，因此可得EP⊥AC；（2）过B作BH⊥GE于H，根据三垂线定理可得∠BPH就是直线BP与平面EFG所成的角．再解三角形可得直线BP与平面EFG所成角的余弦值．

试题解析：(1)证明　设AC交BD于O点，

∵S－ABCD为正四棱锥，

∴SO⊥底面ABCD，BD⊥AC，

又AC平面ABCD，

∴SO⊥AC，∵BD∩SO＝O，

BD平面SBD，SO平面SBD，

∴AC⊥平面SBD，

∵E，F，G分别为BC，SC，CD的中点，

∴FG∥SD，BD∥EG.

又FG∩EG＝G，SD∩BD＝D，

FG平面EFG，EG平面EFG，

SDBSD，BD平面BSD，

∴平面EFG∥平面BSD，

∴AC⊥平面GEF.

又∵PE平面GEF，∴PE⊥AC.

(2)解　过B作BH⊥GE于H，连接PH，

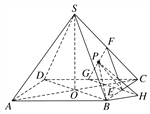
∵BD⊥AC，BD∥GH，

∴BH∥AC，

由(1)知AC⊥平面GEF，

则BH⊥平面GEF.

∴∠BPH就是直线BP与平面EFG所成的角．

在Rt△BHP中，BH＝，PH＝，PB＝，

故cos∠BPH＝＝.

点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.

(1)证明线面、面面平行，需转化为证明线线平行.

(2)证明线面垂直，需转化为证明线线垂直.

(3)证明线线垂直，需转化为证明线面垂直.