Question

【题目】已知是正三棱柱,D是AC中点.

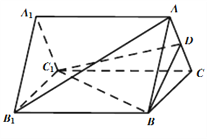
(1)证明: 平面;

(2)若,求二面角的度数.

Answer 1

【答案】(1)见解析(2) .

【解析】试题分析：

本题主要考查线面平行的判定和二面角的求法。(1)连接交于点E，连接ED，根据中位线定理证明∥即可；(2)设，通过建立空间直角坐标系，得到点的坐标后求出平面和平面的法向量，利用两向量的夹角即可得所求。

试题解析：

证明:(1)连接交于点E,连接ED.

因为是矩形,

所以E为中点,

所以为的中位线

所以∥,

又 平面， 平面.

所以∥平面.

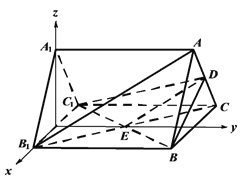
(2)设,建立如图所示的空间直角坐标系xyz,

则,

则

因为，

所以，

解得或（舍去），

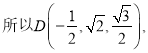
故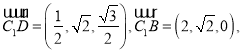

设平面，

由,得.

令，则,

又平面的法向量为,

所以,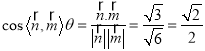

由图形知二面角为锐角，

所以二面角的度数为。