Question

【题目】已知函数f(x)＝在点(1,1)处的切线方程为x＋y＝2.

(1)求a，b的值；

(2)对函数f(x)定义域内的任一个实数x，不等式f(x)－＜0恒成立，求实数m的取值范围．

Answer 1

【答案】（1） （2）m的取值范围是(1，＋∞).

【解析】试题分析：（1）先根据导数几何意义得f′(1)＝－1，再根据 解得a，b的值；（2）先变量分离得 最大值，再利用导数研究函数单调性，进而得最大值，即得实数m的取值范围．

试题解析：(1)由题f′(x)＝，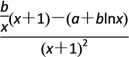

又直线x＋y＝2的斜率为－1.2分

∴f′(1)＝－1，即＝－1.3分

又(1,1)点在函数f(x)＝的图象上，

故＝1，

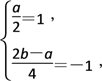由解得

(2)由(1)得f(x)＝ (x＞0)，由f(x)＜及x＞0＜m，8分

令g(x)＝

g′(x)＝

＝，

令h(x)＝1－x－ln xh′(x)＝－1－＜0(x＞0)，故h(x)在区间(0，＋∞)上是减函数，

故当0＜x＜1时，h(x)＞h(1)＝0，

当x＞1时，h(x)＜h(1)＝0.10分

从而当0＜x＜1时，g′(x)＞0，当x＞1时，

g′(x)＜g(x)在(0,1)是增函数，在(1，＋∞)是减函数.11分

故g(x)max＝g(1)＝1，要使＜m成立，只需m＞1，

故m的取值范围是(1，＋∞).