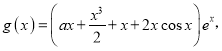题目内容
【题目】已知正![]() 边长为3,点M,N分别是AB,AC边上的点,
边长为3,点M,N分别是AB,AC边上的点,![]() ,如图1所示.将
,如图1所示.将![]() 沿MN折起到
沿MN折起到![]() 的位置,使线段PC长为
的位置,使线段PC长为![]() 连接PB,如图2所示.
连接PB,如图2所示.
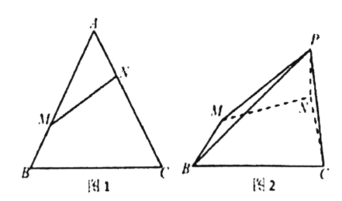
(1)求证:平面![]() 平面BCNM;
平面BCNM;
(2)若点D在线段BC上,且![]() ,求平面PDM和平面PDC所成锐二面角的余弦值.
,求平面PDM和平面PDC所成锐二面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(Ⅰ)推导出AN⊥MN,即PN⊥MN,PN⊥NC,从而PN⊥平面BCNM,由此能证明平面PMN⊥平面BCNM.
(Ⅱ)以N为坐标原点,NM为x轴,NC为y轴,NP为z轴,建立空间直角坐标系,利用向量法能求出二面角M﹣PD﹣C的余弦值.
解:(I)证明:依题意,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由余弦定理,![]() ,
,
解得![]()
根据勾股定理得![]() ,
,
∴![]() ,即
,即![]() ,
,
在图2![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面BCNM,
平面BCNM,
∵![]() 平面PMN,
平面PMN,
∴平面![]() 平面
平面![]() .
.
(2)解:以N为坐标原点,NM为x轴,NC为y轴,NP为z轴,建立空间直角坐标系,
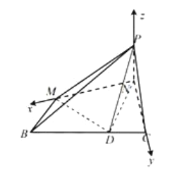
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
设平面MPD的一个法向量![]() ),
),
则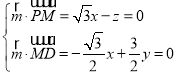 ,取
,取![]() ,
,
得![]() ,
,
设平面PDC的法向量![]() ,
,
则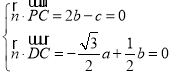 ,
,
取![]() ,得
,得![]() ,
,
设所求角为![]()
∴![]()
![]()
![]() .
.

【题目】随着智能手机的普及,手机计步软件迅速流行开来,这类软件能自动记载每个人每日健步的步数,从而为科学健身提供一定的帮助.某市工会为了解该市市民每日健步走的情况,从本市市民中随机抽取了2000名市民(其中不超过40岁的市民恰好有1000名),利用手机计步软件统计了他们某天健步的步数,并将样本数据分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 九组(单位;千步),将抽取的不超过40岁的市民的样本数据绘制成频率分布直方图如图,将40岁以上的市民的样本数据绘制成频数分布表如下,并利用该样本的频率分布估计总体的概率分布.
九组(单位;千步),将抽取的不超过40岁的市民的样本数据绘制成频率分布直方图如图,将40岁以上的市民的样本数据绘制成频数分布表如下,并利用该样本的频率分布估计总体的概率分布.
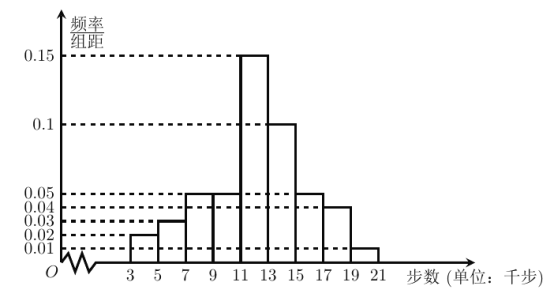
分组(单位 千步) |
|
|
|
|
|
|
|
|
|
频数 | 10 | 20 | 20 | 30 | 400 | 200 | 200 | 100 | 20 |
(1)现规定,日健步步数不低于13000步的为“健步达人”,填写下面列联表,并根据列联表判断能否有99.9%的把握认为是否为“健步达人”与年龄有关;
健步达人 | 非健步达人 | 总计 | |
40岁以上的市民 | |||
不超过40岁的市民 | |||
总计 |
(2)利用样本平均数和中位数估计该市不超过40岁的市民日健步步数(单位:千步)的平均数和中位数;
(3)若日健步步数落在区间![]() 内,则可认为该市民”运动适量”,其中
内,则可认为该市民”运动适量”,其中![]() ,
,![]() 分别为样本平均数和样本标准差,计算可求得频率分布直方图中数据的标准差
分别为样本平均数和样本标准差,计算可求得频率分布直方图中数据的标准差![]() 约为3.64.若一市民某天的健步步数为2万步,试判断该市民这天是否“运动适量”?
约为3.64.若一市民某天的健步步数为2万步,试判断该市民这天是否“运动适量”?
参考公式: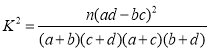
![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |