题目内容
【题目】已知椭圆![]() :
:![]() 的短轴长为2,离心率为
的短轴长为2,离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 且不过点
且不过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(i)若![]() 轴,求直线
轴,求直线![]() 的斜率;
的斜率;
(ii)判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
【答案】(1)![]() ;(2)(i)
;(2)(i)![]() ,(ii)
,(ii)![]() ,理由见解析
,理由见解析
【解析】
(1)根据基本量的关系列式求解即可.
(2) (i)当![]() 轴时,可求得
轴时,可求得![]() 的坐标,进而求得直线
的坐标,进而求得直线![]() 的方程与
的方程与![]() 的坐标,进而求得直线
的坐标,进而求得直线![]() 的斜率.
的斜率.
(ii)联立直线![]() 与椭圆的方程, 设
与椭圆的方程, 设![]() ,
,![]() ,根据题意求出直线
,根据题意求出直线![]() 的方程与
的方程与![]() 的坐标,进而得出直线
的坐标,进而得出直线![]() 的斜率表达式,代入韦达定理的关系化简即可.
的斜率表达式,代入韦达定理的关系化简即可.
(1)由![]() ,
,![]() ,故
,故![]() ,得
,得![]() ,
,![]() ,
,
∴椭圆方程为:![]() ;
;
(2)可设![]() :
:![]() ,
,
①![]() 轴,则
轴,则![]() :
:![]() ,当
,当![]() 在
在![]() 轴上方时有
轴上方时有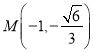 ,
,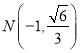 ,
,
∴![]() 的方程为:
的方程为: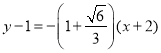 ,∴
,∴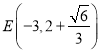 ,
,
∴![]() .
.
当![]() 在
在![]() 轴下方时有
轴下方时有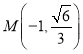 ,
,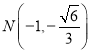 ,
,
∴![]() 的方程为:
的方程为: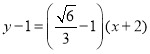 ,∴
,∴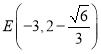 ,
,
∴![]() .
.
综上有![]() .
.
②![]() ,证明如下:
,证明如下:
把![]() 代入
代入![]() 得
得![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
∴![]() :
:![]() ,∴
,∴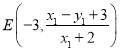 ,
,
∴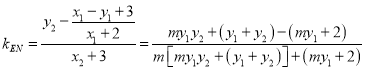 ,
,
由![]() ,∴
,∴![]() ,
,
∴![]() .
.

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案【题目】某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):
锻炼人次 空气质量等级 | [0,200] | (200,400] | (400,600] |
1(优) | 2 | 16 | 25 |
2(良) | 5 | 10 | 12 |
3(轻度污染) | 6 | 7 | 8 |
4(中度污染) | 7 | 2 | 0 |
(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;
(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);
(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?
人次≤400 | 人次>400 | |
空气质量好 | ||
空气质量不好 |
附: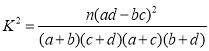 ,
,
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
【题目】在脱贫攻坚中,某市教育局定点帮扶前进村![]() 户贫困户.驻村工作队对这
户贫困户.驻村工作队对这![]() 户村民的贫困程度以及家庭平均受教育程度进行了调査,并将该村贫困户按贫困程度分为“绝对贫困户”与“相对贫困户”,同时按家庭平均受教育程度分为“家庭平均受教育年限
户村民的贫困程度以及家庭平均受教育程度进行了调査,并将该村贫困户按贫困程度分为“绝对贫困户”与“相对贫困户”,同时按家庭平均受教育程度分为“家庭平均受教育年限![]() 年”与“家庭平均受教育年限
年”与“家庭平均受教育年限![]() 年”,具体调査结果如下表所示:
年”,具体调査结果如下表所示:
平均受教育年限 | 平均受教育年限 | 总计 | |
绝对贫困户 | 10 | 40 | 50 |
相对贫困户 | 20 | 30 | 50 |
总计 | 30 | 70 | 100 |
(1)为了参加扶贫办公室举办的贫困户“谈心谈话”活动,现通过分层抽样从“家庭平均受教育年限![]() 年”的
年”的![]() 户贫困户中任意抽取
户贫困户中任意抽取![]() 户,再从所抽取的
户,再从所抽取的![]() 户中随机抽取
户中随机抽取![]() 户参加“谈心谈话”活动,求至少有
户参加“谈心谈话”活动,求至少有![]() 户是绝对贫困户的概率;
户是绝对贫困户的概率;
(2)根据上述表格判断:是否有![]() 的把握认为贫困程度与家庭平均受教育程度有关?
的把握认为贫困程度与家庭平均受教育程度有关?
参考公式:![]()
参考数据:
| 0.050 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |