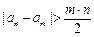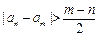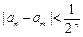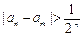题目内容
如果一个数列的各项都是实数,且从第二项开始,每一项与它前一项的平方差是相同的常数,则称该数列为等方差数列,这个常数叫这个数列的公方差.
(1)设数列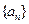 是公方差为
是公方差为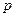 (p>0,an >0)的等方差数列,
(p>0,an >0)的等方差数列,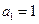 求
求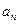 的通项公式;
的通项公式;
(2)若数列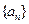 既是等方差数列,又是等差数列,证明该数列为常数列
既是等方差数列,又是等差数列,证明该数列为常数列
(1)设数列
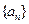 是公方差为
是公方差为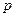 (p>0,an >0)的等方差数列,
(p>0,an >0)的等方差数列,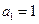 求
求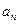 的通项公式;
的通项公式;(2)若数列
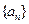 既是等方差数列,又是等差数列,证明该数列为常数列
既是等方差数列,又是等差数列,证明该数列为常数列(1)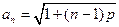 (2)略
(2)略
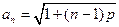 (2)略
(2)略由等方差数列的定义可知: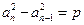
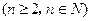 ,
,
由此可得: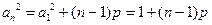
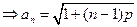
(2)证法一:∵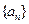 是等差数列,设公差为
是等差数列,设公差为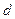 ,则
,则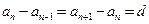
又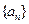 是等方差数列,∴
是等方差数列,∴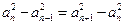 ……………8分
……………8分
∴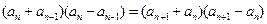
即 ,……….10分
,……….10分
∴ ,即
,即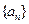 是常数列.………………12分
是常数列.………………12分
证法二:∵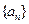 是等差数列,设公差为
是等差数列,设公差为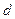 ,则
,则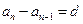 ……1
……1
又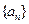 是等方差数列,设公方差为
是等方差数列,设公方差为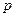 ,则
,则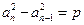 ……2………….8分
……2………….8分
1代入2得,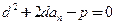 ……3
……3
同理有,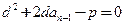 ……4………….10分
……4………….10分
两式相减得:即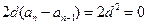 ,
,
∴ ,即
,即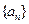 是常数列.…………..12分
是常数列.…………..12分
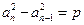
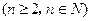 ,
,由此可得:
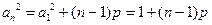
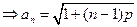
(2)证法一:∵
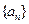 是等差数列,设公差为
是等差数列,设公差为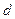 ,则
,则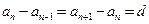
又
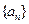 是等方差数列,∴
是等方差数列,∴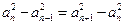 ……………8分
……………8分∴
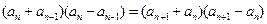
即
 ,……….10分
,……….10分∴
 ,即
,即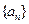 是常数列.………………12分
是常数列.………………12分证法二:∵
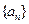 是等差数列,设公差为
是等差数列,设公差为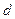 ,则
,则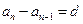 ……1
……1又
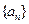 是等方差数列,设公方差为
是等方差数列,设公方差为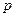 ,则
,则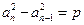 ……2………….8分
……2………….8分1代入2得,
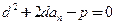 ……3
……3同理有,
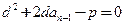 ……4………….10分
……4………….10分两式相减得:即
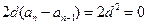 ,
,∴
 ,即
,即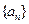 是常数列.…………..12分
是常数列.…………..12分
练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
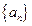 中,
中,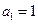 ,
,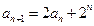 ;
;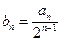 .证明:数列
.证明:数列 是等差数列;(2)求数列
是等差数列;(2)求数列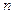 项和
项和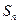 。
。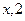 ),b =(
),b =(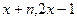 )(
)(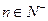 ),函数
),函数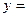 a·b在[0,1]上的最小值与最大值的和为
a·b在[0,1]上的最小值与最大值的和为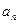 ,又数列{
,又数列{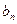 }满足:
}满足: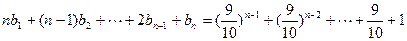 .
.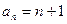 ;
;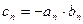 ,试问数列{
,试问数列{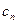 }中,是否存在正整数
}中,是否存在正整数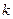 ,使得对于任意的正整数
,使得对于任意的正整数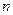 ,都有
,都有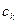 成立?证明你的结论.
成立?证明你的结论.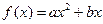 +
+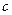 的图象通过原点,对称轴为
的图象通过原点,对称轴为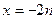 ,
,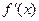 是
是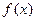 的导函数,且
的导函数,且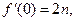
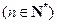 .
.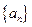 满足
满足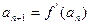 ,且
,且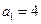 ,求数列
,求数列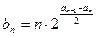 ,
,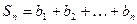 ,是否存在自然数M,使得当
,是否存在自然数M,使得当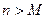 时
时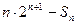
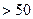 恒成立?若存在,求出最小的M;若不存在,说明理由.
恒成立?若存在,求出最小的M;若不存在,说明理由.
 小题满分14分)已知
小题满分14分)已知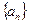 是正数组成的数列,
是正数组成的数列,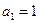 ,且点(
,且点(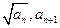 )(n
)(n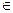 N*)在
N*)在 函数
函数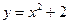 的图象上.(Ⅰ)求数列
的图象上.(Ⅰ)求数列 (Ⅱ)若
(Ⅱ)若
 数列
数列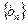
 满足
满足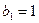 ,
,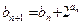 ,求数列
,求数列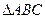 分割成
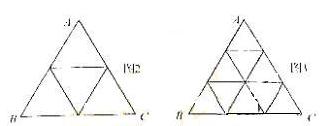
分割成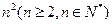 个全等的小正三角形(图2,图3分别给出了n="2," 3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列.若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为
个全等的小正三角形(图2,图3分别给出了n="2," 3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列.若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为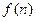 ,则有
,则有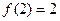 ,
,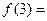 ,… ,
,… ,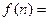 .
.
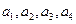 成等差数列,且
成等差数列,且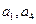 为方程方程
为方程方程 的两根,则
的两根,则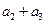 等于 。
等于 。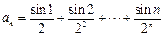 ,则对任意正整数
,则对任意正整数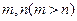 都成立的是( )
都成立的是( )