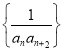题目内容
【题目】已知椭圆C: ![]() =1(a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为
=1(a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为 ![]() b.
b.
(1)求椭圆C的离心率;
(2)设b=2,直线y=kx+4与椭圆C交于不同的两点M,N,求证:直线BM与直线AN的交点G在定直线上.
【答案】
(1)解:设F的坐标为(﹣c,0),依题意有bc= ![]() ab,
ab,
∴椭圆C的离心率e= ![]() =
= ![]() .
.
(2)解:若b=2,由(1)得a=2 ![]() ,∴椭圆方程为
,∴椭圆方程为 ![]() .
.
联立方程组 ![]()
化简得:(2k2+1)x2+16kx+24=0,
由△=32(2k2﹣3)>0,解得:k2> ![]()
由韦达定理得:xM+xN= ![]() …①,xMxN=
…①,xMxN= ![]() …②
…②
设M(xM,kxM+4),N(xN,kxN+4),
MB方程为:y= ![]() x﹣2,…③
x﹣2,…③
NA方程为:y= ![]() x+2,…④
x+2,…④
由③④解得:y= ![]()
= 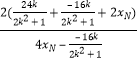 =
= 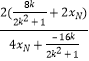 =1
=1
即yG=1,
∴直线BM与直线AN的交点G在定直线上
【解析】(1)设F的坐标为(﹣c,0),原点O到直线FA的距离为 ![]() b,列出方程,即可求解椭圆的离心率.(2)求出椭圆方程,联立方程组
b,列出方程,即可求解椭圆的离心率.(2)求出椭圆方程,联立方程组 ![]() ,通过韦达定理,设M(xM , kxM+4),N(xN , kxN+4),
,通过韦达定理,设M(xM , kxM+4),N(xN , kxN+4),
求出MB方程,NA方程,求出交点坐标,推出结果.
【考点精析】通过灵活运用椭圆的标准方程,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 即可以解答此题.
即可以解答此题.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案【题目】某社区为丰富居民节日活动,组织了“迎新春”象棋大赛,已知报名的选手情况统计如下表:
组别 | 男 | 女 | 总计 |
中年组 |
|
| 91 |
老年组 | 16 |
|
|
已知中年组女性选手人数是仅比老年组女性选手人数多2人,若对中年组和老年组分别利用分层抽样的方法抽取部分报名者参加比赛,已知老年组抽取了5人,其中女性3人,中年组抽取了7人.
(1)求表格中的数据![]() ;
;
(2)若从选出的中年组的选手中随机抽取两名进行比赛,求至少有一名女性选手的概率.