题目内容
12.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线与圆x2+y2-4x+2=0,有公共点,则该双曲线离心率的取值范围是( )| A. | (1,2] | B. | [$\sqrt{2}$,+∞) | C. | (1,$\sqrt{2}$] | D. | (1,$\sqrt{2}$) |
分析 双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线与圆x2+y2-4x+2=0有交点?圆心(2,0)到渐近线的距离≤半径r.解出即可.
解答 解:由圆x2+y2-4x+2=0化为(x-2)2+y2=2,得到圆心(2,0),半径r=$\sqrt{2}$.
∵双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线y=±$\frac{b}{a}$x与圆x2+y2-4x+2=0有交点,
∴$\frac{|2b|}{\sqrt{{a}^{2}+{b}^{2}}}$≤$\sqrt{2}$,化为b2≤a2.
∴1<e<$\frac{c}{a}$≤$\sqrt{2}$.
∴该双曲线的离心率的取值范围是(1,$\sqrt{2}$].
故选:C.
点评 熟练掌握双曲线的渐近线方程、离心率的计算公式、圆的标准方程、直线与圆的位置关系、点到直线的距离公式是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
4.函数y=2sinx,x∈[0,2π]与y=$\frac{3}{2}$的交点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
17.如图所示的框图输出结果为( )


| A. | 1023 | B. | 1024 | C. | 511 | D. | 2047 |
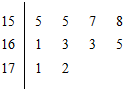 如图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个数数字,从图中可以得到这10位同学身高的中位数是162.
如图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个数数字,从图中可以得到这10位同学身高的中位数是162.