题目内容
(本小题15分)
已知函数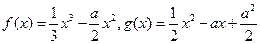 。
。
(I)当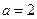 时,求曲线
时,求曲线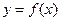 在点
在点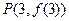 处的切线方程;
处的切线方程;
(Ⅱ)当函数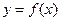 在区间
在区间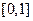 上的最小值为
上的最小值为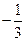 时,求实数
时,求实数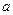 的值;
的值;
(Ⅲ)若函数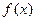 与
与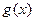 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数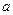 的取值范围。
的取值范围。
已知函数
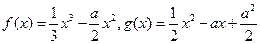 。
。(I)当
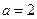 时,求曲线
时,求曲线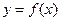 在点
在点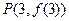 处的切线方程;
处的切线方程;(Ⅱ)当函数
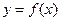 在区间
在区间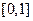 上的最小值为
上的最小值为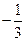 时,求实数
时,求实数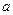 的值;
的值;(Ⅲ)若函数
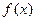 与
与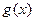 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数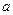 的取值范围。
的取值范围。(I)因为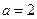 ,由题意
,由题意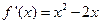 (2分)
(2分)
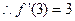 即过点
即过点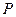 的切线斜率为3,又点
的切线斜率为3,又点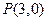
则过点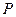 的切线方程为:
的切线方程为: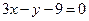 (5分)
(5分)
(Ⅱ)右题意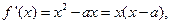 令
令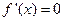 得
得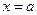 或
或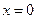 (6分)
(6分)
由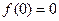 ,要使函数
,要使函数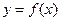 在区间
在区间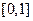 上的最小值为
上的最小值为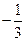 ,则
,则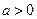
(i)当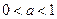 时,
时,
当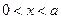 时,
时,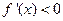 ,当
,当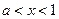 时,
时,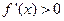 ,
,
所以函数
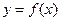 在区间[0,1]上,
在区间[0,1]上,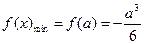
即: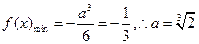 ,舍去 (8分)
,舍去 (8分)
(ii)当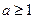 时,
时,
当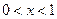 时,
时,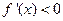 ,则使函数
,则使函数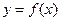 在区间
在区间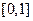 上单调递减,
上单调递减,
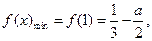
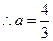
综上所述: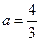 (10分)
(10分)
(Ⅲ)设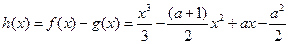
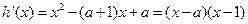
令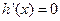 得
得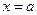 或
或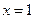 (11分)
(11分)
(i)当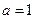 时,函数
时,函数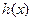 单调递增,函数
单调递增,函数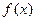 与
与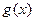 的图象不可能有三个不同的交点
的图象不可能有三个不同的交点
(ii)当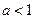 时,
时,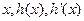 随
随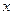 的变化情况如下表:
的变化情况如下表:
欲使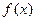 与
与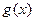 图象有三个不同的交点,
图象有三个不同的交点,
方程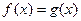 ,也即
,也即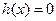 有三个不同的实根
有三个不同的实根
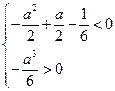 ,所以
,所以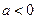 (13分)
(13分)
(iii)当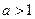 时,
时,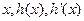 随
随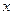 的变化情况如下表:
的变化情况如下表:
由于极大值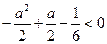 恒成立,故此时不能有三个解
恒成立,故此时不能有三个解
综上所述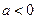 (15分)
(15分)
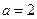 ,由题意
,由题意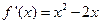 (2分)
(2分)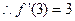 即过点
即过点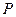 的切线斜率为3,又点
的切线斜率为3,又点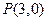
则过点
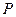 的切线方程为:
的切线方程为: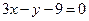 (5分)
(5分)(Ⅱ)右题意
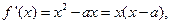 令
令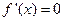 得
得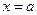 或
或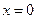 (6分)
(6分)由
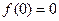 ,要使函数
,要使函数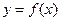 在区间
在区间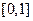 上的最小值为
上的最小值为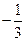 ,则
,则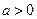
(i)当
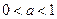 时,
时,当
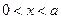 时,
时,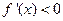 ,当
,当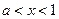 时,
时,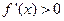 ,
,所以函数

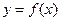 在区间[0,1]上,
在区间[0,1]上,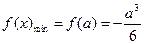
即:
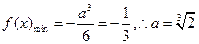 ,舍去 (8分)
,舍去 (8分)(ii)当
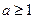 时,
时,当
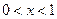 时,
时,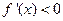 ,则使函数
,则使函数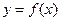 在区间
在区间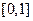 上单调递减,
上单调递减,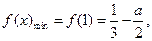
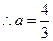
综上所述:
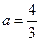 (10分)
(10分)(Ⅲ)设
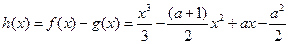
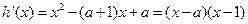
令
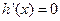 得
得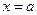 或
或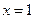 (11分)
(11分)(i)当
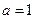 时,函数
时,函数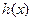 单调递增,函数
单调递增,函数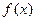 与
与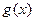 的图象不可能有三个不同的交点
的图象不可能有三个不同的交点(ii)当
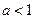 时,
时,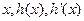 随
随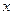 的变化情况如下表:
的变化情况如下表: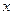 | 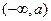 | 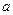 | 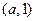 | 1 | 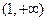 |
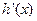 | + | 0 | 一 | 0 | + |
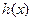 |  | 极大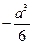 |  | 极小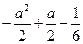 |  |
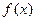 与
与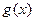 图象有三个不同的交点,
图象有三个不同的交点,方程
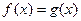 ,也即
,也即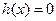 有三个不同的实根
有三个不同的实根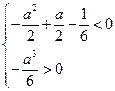 ,所以
,所以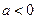 (13分)
(13分)(iii)当
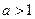 时,
时,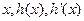 随
随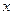 的变化情况如下表:
的变化情况如下表: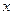 | 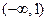 | 1 | 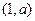 | 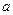 | 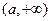 |
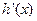 | + | 0 | 一 | 0 | + |
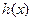 |  | 极大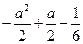 |  | 极小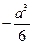 |  |
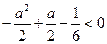 恒成立,故此时不能有三个解
恒成立,故此时不能有三个解综上所述
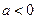 (15分)
(15分)略

练习册系列答案
相关题目
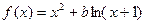
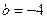 时,求函数
时,求函数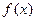 的极
的极 值;
值; 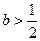 时,求函数
时,求函数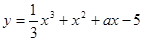 (1)若函数在
(1)若函数在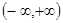 总是单调函数,则
总是单调函数,则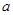 的取值范围是 . (2)若函数在
的取值范围是 . (2)若函数在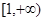 上总是单调函数,则
上总是单调函数,则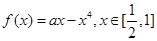 ,A、B是图像上不同的两点,若直线AB的斜率k总满足
,A、B是图像上不同的两点,若直线AB的斜率k总满足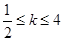 ,则实数a的值是 ( )
,则实数a的值是 ( )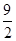 B.
B.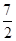 C.5 D.1
C.5 D.1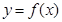 在点
在点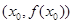 处的 切线方程为
处的 切线方程为 ,则( )
,则( )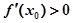
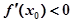
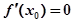
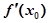 不存在
不存在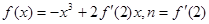 ,则二项式
,则二项式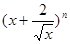 展开式中常数
展开式中常数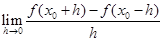 =( )
=( )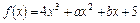 的图象在
的图象在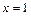 处的切线方程为
处的切线方程为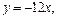
 求函
求函 数
数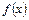 的解析式;
的解析式;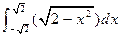 = 。
= 。