题目内容
已知函数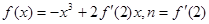 ,则二项式
,则二项式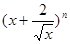 展开式中常数
展开式中常数
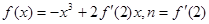 ,则二项式
,则二项式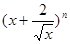 展开式中常数
展开式中常数| A.第6项 | B.第7项 | C.第8项 | D.第9项 |
D
分析:根据题意,对f(x)求导,有f′(x)=-3x2+2f′(2),令x=2,有f′(2)=-12+2f′(2),解可得n=f′(2)=12,将n=12代入(x+
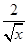 )n的二项展开式,则可得满足常数项的r的值,进而可得答案.
)n的二项展开式,则可得满足常数项的r的值,进而可得答案.解:根据题意,f′(x)=-3x2+2f′(2),
令x=2,有f′(2)=-12+2f′(2),
进而有n=f′(2)=12,
则(x+
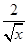 )n的二项展开式为Tr+1=C12r(x)12-r(
)n的二项展开式为Tr+1=C12r(x)12-r(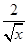 )r=C12r?(2r)?x(
)r=C12r?(2r)?x( ),
),令12-
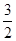 r=0,解可得,r=8,
r=0,解可得,r=8,此时为展开式的第9项,
故选D.

练习册系列答案
相关题目
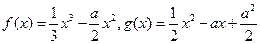 。
。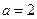 时,求曲线
时,求曲线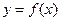 在点
在点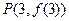 处的切线方程;
处的切线方程;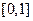 上的最小值为
上的最小值为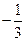 时,求实数
时,求实数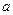 的值;
的值;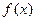 与
与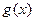 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数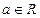 ,函数
,函数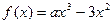 .
.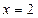 是函数
是函数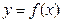 的极值点,求实数
的极值点,求实数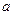 的值;
的值;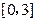 上的最大值和最小值;
上的最大值和最小值;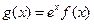 在
在 上是单调递减函数,求实数
上是单调递减函数,求实数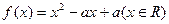 ,在定义域内有且只有一个零点,存在
,在定义域内有且只有一个零点,存在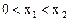 , 使得不等式
, 使得不等式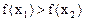 成立. 若
成立. 若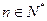 ,
,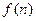 是数列
是数列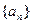 的前
的前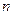 项和.
项和.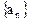 的通项公式;
的通项公式;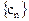 中,所有满足
中,所有满足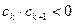 的正整数
的正整数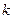 的个数称为这个数列
的个数称为这个数列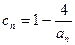 (n为正整数),求数列
(n为正整数),求数列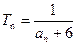 (
(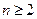 且
且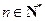 ),使不等式
),使不等式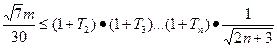 恒成立,求正整数
恒成立,求正整数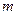 的最大值
的最大值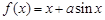 在
在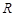 上递增,则实数
上递增,则实数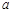 的取值范围是 .
的取值范围是 .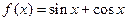 在点
在点 处的切线方程为
处的切线方程为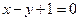
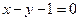
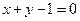
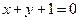
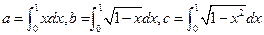 ,则
,则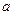 ,
,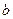 ,
, 的大小关系是( )
的大小关系是( )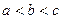
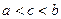

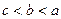
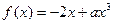 ,若
,若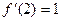 ,则
,则 ( )
( )