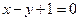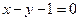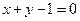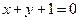题目内容
(满分10分)设函数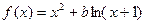
(1) 当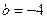 时,求函数
时,求函数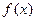 的极
的极 值;
值;
(2) 当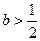 时,求函数
时,求函数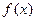 在定义域内的单调性.
在定义域内的单调性.
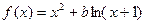
(1) 当
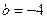 时,求函数
时,求函数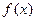 的极
的极 值;
值; (2) 当
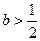 时,求函数
时,求函数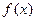 在定义域内的单调性.
在定义域内的单调性.解:由题可知函数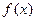 的定义域为
的定义域为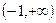
(1)当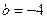 时,
时, ,
,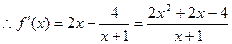
令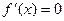 ,得
,得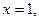 或
或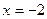 ,由定义域
,由定义域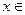
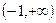 得
得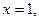
当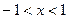 时,
时,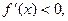 当
当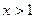 时,
时,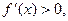
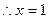 是极小值点
是极小值点
 ………………………………5分
………………………………5分
(2)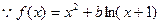 ,
,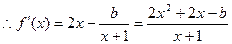
令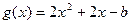 ,方程
,方程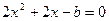
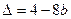 。
。
当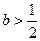 时,
时,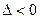 ,
,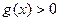 恒成立。又由定义域
恒成立。又由定义域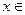
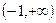 得
得
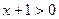 即
即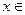
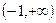 时
时
所以函数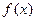 在定义域内为增函数。 ……………………………10分
在定义域内为增函数。 ……………………………10分
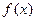 的定义域为
的定义域为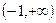
(1)当
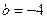 时,
时, ,
,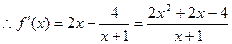
令
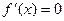 ,得
,得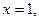 或
或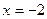 ,由定义域
,由定义域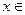
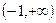 得
得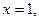
当
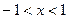 时,
时,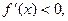 当
当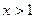 时,
时,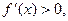
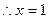 是极小值点
是极小值点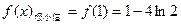 ………………………………5分
………………………………5分(2)
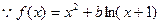 ,
,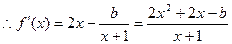
令
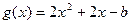 ,方程
,方程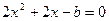
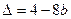 。
。当
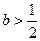 时,
时,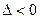 ,
,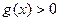 恒成立。又由定义域
恒成立。又由定义域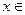
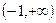 得
得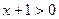 即
即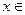
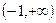 时
时
所以函数
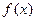 在定义域内为增函数。 ……………………………10分
在定义域内为增函数。 ……………………………10分略

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
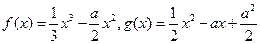 。
。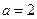 时,求曲线
时,求曲线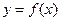 在点
在点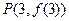 处的切线方程;
处的切线方程;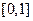 上的最小值为
上的最小值为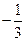 时,求实数
时,求实数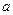 的值;
的值;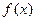 与
与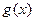 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数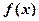 是定义在实数集
是定义在实数集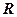 上的不恒为零的偶函数,
上的不恒为零的偶函数,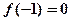 ,且对任意实数
,且对任意实数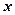 都
都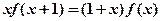 ,则
,则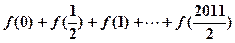 的值是
的值是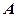 .
.

 .
. 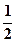
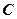 .
. 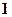
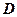 .
.
 ,
, .
. 在
在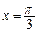 时取得极值,求
时取得极值,求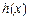 的单调递减区间;
的单调递减区间;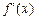 |≤| x |;
|≤| x |;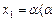 ∈[
∈[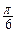 ,
,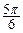 ]),
]),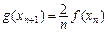 ,求证:
,求证: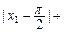
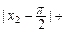 …+
…+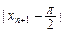 <
<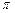 (n∈N*).
(n∈N*). 轴和
轴和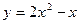 所围成的图形的面积为( )
所围成的图形的面积为( )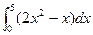
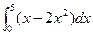
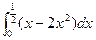
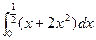
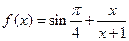
 ,则
,则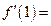
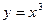 +2在
+2在
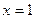 处的切线方程是 ______ ________.
处的切线方程是 ______ ________.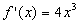 ,f(2 )=14,则此函数为 ( )
,f(2 )=14,则此函数为 ( )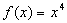
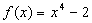
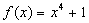
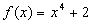
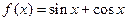 在点
在点 处的切线方程为
处的切线方程为