题目内容
【题目】已知抛物线![]() ,过焦点F的直线l与抛物线分别交于A、B两点,O为坐标原点,且
,过焦点F的直线l与抛物线分别交于A、B两点,O为坐标原点,且![]() .
.
(1)求抛物线的标准方程;
(2)对于抛物线上任一点Q,点P(2t,0)都满足|PQ|≥2|t|,求实数t的取值范围.
【答案】(1) ![]() ;(2)(﹣∞,
;(2)(﹣∞,![]() ]
]
【解析】
(1)设出过焦点F的直线l的方程,与抛物线方程联立,利用一元二次方程根与系数关系,结合![]() ,可以求出抛物线的标准方程;
,可以求出抛物线的标准方程;
(2)设出点Q坐标,根据|PQ|≥2|t|,根据点Q横坐标的取值范围,结合不等式的性质可以求出实数t的取值范围.
(1)抛物线![]() 的焦点F(
的焦点F(![]() ,0),设直线l的方程为x=my
,0),设直线l的方程为x=my![]() ,
,
设A(x1,y1),B(x2,y2),联立抛物线方程可得y2﹣2pmy﹣p2=0,
可得![]() ,
,
则 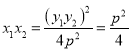 ,
,
由![]() ,可得
,可得![]()
解得p![]() ,即抛物线的方程为y2=x;
,即抛物线的方程为y2=x;
(2)设点Q的坐标为(x0,y0),有y02=x0,
由|PQ|≥2|t|,即![]() 2|t|,整理可得x02﹣4tx0+y02≥0,
2|t|,整理可得x02﹣4tx0+y02≥0,
即x02﹣4tx0+x0≥0,可得x0(x0﹣4t+1)≥0,
由x0≥0,可得x0﹣4t+1≥0,即1﹣4t≥0,可得t![]() ,
,
则t的取值范围是(﹣∞,![]() ].
].

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
