题目内容
7. 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=$\sqrt{3}$,BC=1,AA1=AC=2,E、F分别为A1C1、BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=$\sqrt{3}$,BC=1,AA1=AC=2,E、F分别为A1C1、BC的中点.(1)求证:平面ABE⊥平面B1BCC1;
(2)求证:C1F∥平面ABE;
(3)求多面体A1B1C1-ABF的体积.
分析 (1)在三棱柱ABC-A1B1C1中,BB1⊥底面ABC,可得BB1⊥AB,由于AB=$\sqrt{3}$,BC=1,AC=2,可得AB⊥BC,利用线面垂直的判定定理可得:AB⊥平面B1BCC1,即可证明平面ABE⊥平面B1BCC1;
(2)取AB的中点G,连接EG,FG,利用三角形中位线定理可得:FG∥AC,$FG=\frac{1}{2}AC$,于是$FG\underset{∥}{=}E{C}_{1}$,可得FGEC1为平行四边形,得到C1F∥EG,即可证明C1F∥平面ABE;
(3)利用多面体A1B1C1-ABF的体积V=${V}_{{A}_{1}{B}_{1}{C}_{1}-ABC}$-${V}_{{C}_{1}-ACF}$即可得出.
解答  (1)证明:在三棱柱ABC-A1B1C1中,BB1⊥底面ABC,
(1)证明:在三棱柱ABC-A1B1C1中,BB1⊥底面ABC,
∴BB1⊥AB,
∵AB=$\sqrt{3}$,BC=1,AC=2,
∴AB⊥BC,
∵BC∩BB1=B,∴AB⊥平面B1BCC1,
又AB?平面ABE,
∴平面ABE⊥平面B1BCC1;
(2)证明:取AB的中点G,连接EG,FG,
∵E,F分别是A1C1,BC的中档,
∴FG∥AC,$FG=\frac{1}{2}AC$,
∵$AC\underset{∥}{=}{A}_{1}{C}_{1}$,∴$FG\underset{∥}{=}E{C}_{1}$,
∴FGEC1为平行四边形,
∴C1F∥EG,
又EG?平面ABE,C1F?平面ABE,
∴C1F∥平面ABE;
(3)解:多面体A1B1C1-ABF的体积V=${V}_{{A}_{1}{B}_{1}{C}_{1}-ABC}$-${V}_{{C}_{1}-ACF}$=$\frac{5\sqrt{3}}{6}$.
点评 本题主要考查直线与直线、直线与平面的位置关系、平行四边形的性质、体积等基础知识,考查空间想象能力、推理论证能力、运算求解能力、化归与转化能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案
| A. | A1C1∥AD | B. | C1D1⊥AB | ||
| C. | AC1与CD成45°角 | D. | A1C1与B1C成60°角 |

| A. | 8 | B. | $\frac{8}{3}$$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
 已知一个几何体的三视图如图所示,则这个几何体的体积为$\frac{22}{3}$.
已知一个几何体的三视图如图所示,则这个几何体的体积为$\frac{22}{3}$. 正三棱柱ABC-A1B1C1中,AB=2.AA1=3,点E为BB1中点,
正三棱柱ABC-A1B1C1中,AB=2.AA1=3,点E为BB1中点,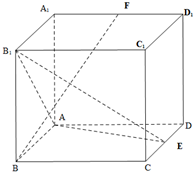 如图:在长方体ABCD-A1B1C1D1中,AB=2,BC=4,BB1=4,E是CD的中点,F是A1D1的中点.
如图:在长方体ABCD-A1B1C1D1中,AB=2,BC=4,BB1=4,E是CD的中点,F是A1D1的中点.