题目内容
17.已知函数f(x)=ex,这里e为自然对数的底数.(1)求函数y=f(x)-x的单调区间;
(2)当x>0时,证明:f(x)-x+ln$\frac{f(x)}{x}$>2;
(3)若当x≤0时,f(-x)-1+x-$\frac{a}{2}$x2≥0恒成立,求实数a的取值范围.
分析 (1)求出原函数的导函数,得到导函数的零点,由零点对定义域分段,然后利用导函数在各区间段的符号求函数的单调期间;
(2)把证$f(x)-x+ln\frac{f(x)}{x}>2$转化为ex-x+x-lnx>2,然后令${f}_{1}(x)={e}^{x}-x$,f2(x)=x-lnx,由导函数求得两函数的最小值后得答案;
(3)把f(-x)代入f(-x)-1+x-$\frac{a}{2}$x2≥0,题转化为:当x≤0时,h(x)≥0恒成立,求实数a的取值范围,令$h(x)={e}^{-x}-1+x-\frac{a}{2}{x}^{2}$,求其导函数,结合(1)中ex≥1+x,通过放缩可得使x≤0时,满足h′(x)≤0的a的范围为a≤1,当a>1时,通过放缩可得当x∈(-lna,0)时,h′(x)≥(1-ex)(-e-x+a)>0,说明h(x)在(-lna,0)上单调递增,得到当x∈(-lna,0)时,h(x)<h(0)=0,说明不满足对任意x≤0,有f(-x)-1+x-$\frac{a}{2}$x2≥0恒成立,从而求得实数a的取值范围.
解答 (1)解:由y=f(x)-x=ex-x,得y′=ex-1,
由y′=ex-1>0,得x>0,由y′=ex-1<0,得x<0.
∴函数y=f(x)-x的单调减区间为(-∞,0),单调增区间为(0,+∞);
(2)证明:要证$f(x)-x+ln\frac{f(x)}{x}>2$,即证ex-x+x-lnx>2.
令${f}_{1}(x)={e}^{x}-x$.
由(1),当x>0时,f1(x)>f1(0)=1,即ex-x>1.①
令f2(x)=x-lnx,则${{f}_{2}}^{′}(x)=1-\frac{1}{x}=\frac{x-1}{x}$.
当0<x<1时,${{f}_{2}}^{′}(x)<0$;当x>1时,${{f}_{2}}^{′}(x)>0$.
∴f2(x)在(0,1)上为减函数,在(1,+∞)上为增函数.
∴当x>0时,f2(x)≥f2(1)=1,即x-lnx≥1.②
①②两式相加得ex-x+x-lnx>2;
(3)解:f(-x)-1+x-$\frac{a}{2}$x2≥0,即为${e}^{-x}-1+x-\frac{a}{2}{x}^{2}≥0$.
令$h(x)={e}^{-x}-1+x-\frac{a}{2}{x}^{2}$,则h′(x)=-e-x+1-ax.
问题转化为:当x≤0时,h(x)≥0恒成立,求实数a的取值范围.
由(1)知ex≥1+x,当且仅当x=0时取等号.
故e-x≥1-x,
∴-e-x+1≤x,当且仅当x=0时取等号.
∴h′(x)=-e-x+1-ax≤x-ax=(1-a)x,当且仅当x=0时取等号.
当1-a≥0时,则a≤1.
从而,当x≤0时,h′(x)≤0,当且仅当a=1,且x=0时取等号.
∴h(x)在(-∞,0]上单调递减,
∴h(x)≥h(0)=0.
由(1)知ex≥1+x,∴x≤ex-1.
∴-x≥1-ex,当且仅当x=0时取等号.
当a>1时,h′(x)=-e-x+1-ax≥-e-x+1+a(1-ex)=(1-ex)(-e-x+a).
令-e-x+a>0,得e-x<a,即x>-lna.
从而,当x∈(-lna,0)时,h′(x)≥(1-ex)(-e-x+a)>0.
∴h(x)在(-lna,0)上单调递增.
∴当x∈(-lna,0)时,h(x)<h(0)=0.
可见,a>1不满足题意.
综上,所求实数a的取值范围为(-∞,1].
点评 本题考查利用导数研究函数的单调区间,考查了利用导数求函数的最值,考查不等式恒成立时所取的条件,着重考查了数学转化思想方法,属难题.

| A. | (0,$\frac{π}{6}$] | B. | [$\frac{π}{3}$,$\frac{2π}{3}$] | C. | (0,$\frac{π}{3}$] | D. | [$\frac{2π}{3}$,π) |
 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=$\sqrt{3}$,BC=1,AA1=AC=2,E、F分别为A1C1、BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=$\sqrt{3}$,BC=1,AA1=AC=2,E、F分别为A1C1、BC的中点.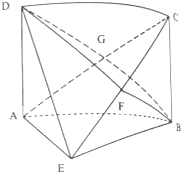 如图,在四棱锥E-ABCD中,地面ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC与BD相交于点G.
如图,在四棱锥E-ABCD中,地面ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC与BD相交于点G. 如图1,在Rt△ABC中,∠ABC=90°,∠BAC=60°,AB=2,D,E分别为AC,BD的中点,连接AE并延长BC于F,将△ABD沿BD折起,使平面ABD⊥平面BCD,如图2,所示,
如图1,在Rt△ABC中,∠ABC=90°,∠BAC=60°,AB=2,D,E分别为AC,BD的中点,连接AE并延长BC于F,将△ABD沿BD折起,使平面ABD⊥平面BCD,如图2,所示, 如图所示的一块木料中,棱BC平行于面A′C′.
如图所示的一块木料中,棱BC平行于面A′C′.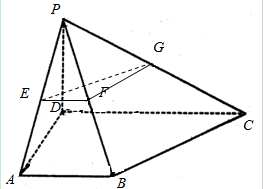 如图,在四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}$AD=1.
如图,在四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}$AD=1.