题目内容
8.已知函数f(x)=|x2-2x-3|,x∈R.(1)直线y=m与y=f(x)的图象从左到右依次有4个交点A、B、C、D,若线段AB、BC、CD能构成三角形,求m的取值范围;
(2)当函数f(x)的定义域为[a,b]时,值域恰好为[$\frac{5}{3}$(a-1),$\frac{5}{3}$(b-1)],求a、b的值.
分析 (1)首先画出f(x)和y=m的图象,根据图象即可求得A,B,C,D四点坐标,进而求出|AB|,|CD|,|BC|,而若线段AB、BC、CD能构成三角形只要满足|AB|+|CD|>|BC|即可,这样便可求出m的范围;
(2)结合图形,对应区间[a,b]的位置分成①[a,b]⊆(-∞,-1),(-1,1),(1,3),(3,+∞),②在[a,b]上取到最小值0,③在[a,b]上取到最大值f(1),这样求出每种情况的a,b即可得到a,b的值.
解答 解:f(x)的图象如下,
通过解方程|x2-2x-3|=m得到A,B,C,D四点的横坐标如下:
1-$\sqrt{4+m}$,$1-\sqrt{4-m}$,$1+\sqrt{4-m},1+\sqrt{4+m}$;
∴$|AB|=|CD|=\sqrt{4+m}-\sqrt{4-m}$,$|BC|=2\sqrt{4-m}$;
要使AB,BC,CD能构成三角形,只要|AB|+|CD|>|BC|;
∴$2(\sqrt{4+m}-\sqrt{4-m})>2\sqrt{4-m}$;
∴$\sqrt{4+m}>2\sqrt{4-m}$;
∴得到$\left\{\begin{array}{l}{4-m>0}\\{4+m>4(4-m)}\end{array}\right.$;
解得$\frac{12}{5}<m<4$;
∴m的取值范围为($\frac{12}{5},4$);
(2)①若[a,b]⊆(-∞,-1),f(x)在[a,b]上单调递减;
∴f(x)的值域为[f(b),f(a)]=[b2-2b-3,a2-2a-3]=[$\frac{5}{3}(a-1),\frac{5}{3}(b-1)$];
∴$\left\{\begin{array}{l}{{b}^{2}-2b-3=\frac{5}{3}(a-1)}\\{{a}^{2}-2a-3=\frac{5}{3}(b-1)}\end{array}\right.$;
两式相减得$a+b=\frac{1}{3}$,∵此时a+b<-2,所以这种情况不存在;
同样的办法可以判断当[a,b]⊆(-1,1),(1,3),(3,+∞)时也不存在;
②若f(x)在[a,b]上的最小值为0时;
则a=1,则b≥3;
若此时f(x)的最大值为f(1)=4=$\frac{5}{3}(b-1)$,则b=$\frac{17}{5}>3$,符合条件;
若此时f(x)的最大值为f(b)=${b}^{2}-2b-3=\frac{5}{3}(b-1)$,解得b=4,或b=$-\frac{1}{3}$(舍去),b=4符合条件;
∴在这种情况下a=1,b=$\frac{17}{5},或4$;
③若f(x)在[a,b]上的最大值为f(1)=4=$\frac{5}{3}(b-1)$,b=$\frac{17}{5}$,则此时最小值一定是0=$\frac{5}{3}(a-1)$,a=1;
∴综上得a=1,b=$\frac{17}{5}$,或4.
点评 考查直线y=b和曲线f(x)交点的横坐标和方程f(x)=b解的关系,求根公式求一元二次方程的根,三条线段构成三角形的条件:两边之和大于第三边,分类讨论的方法,以及结合图形解题的方法,根据函数的单调性求函数的值域.

 如图,在四棱锥ABCD中,点E、F、G分别为棱BC、BD、CD的中点,且AB=AG,BC=BD.
如图,在四棱锥ABCD中,点E、F、G分别为棱BC、BD、CD的中点,且AB=AG,BC=BD. 在四棱锥P-ABCD中,底面ABCD是平行四边形,E为PD的中点,点F在棱PD上,且FD=$\frac{1}{3}$PD.
在四棱锥P-ABCD中,底面ABCD是平行四边形,E为PD的中点,点F在棱PD上,且FD=$\frac{1}{3}$PD. 如图,BC是圆O的一条弦,延长BC至点E,使得BC=2CE=2,过E作圆O的切线,A为切点,∠BAC的平分线AD交BC于点D,则DE的长为$\sqrt{3}$.
如图,BC是圆O的一条弦,延长BC至点E,使得BC=2CE=2,过E作圆O的切线,A为切点,∠BAC的平分线AD交BC于点D,则DE的长为$\sqrt{3}$.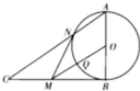 如图,在Rt△ABC中,∠ABC=90°,以AB为直径作圆O与斜边AB交于N,过点O作OM∥AC,交BC于M,交圆O于Q.
如图,在Rt△ABC中,∠ABC=90°,以AB为直径作圆O与斜边AB交于N,过点O作OM∥AC,交BC于M,交圆O于Q. 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=$\sqrt{3}$,BC=1,AA1=AC=2,E、F分别为A1C1、BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=$\sqrt{3}$,BC=1,AA1=AC=2,E、F分别为A1C1、BC的中点.