题目内容
12.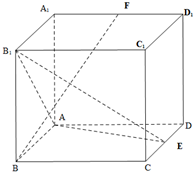 如图:在长方体ABCD-A1B1C1D1中,AB=2,BC=4,BB1=4,E是CD的中点,F是A1D1的中点.
如图:在长方体ABCD-A1B1C1D1中,AB=2,BC=4,BB1=4,E是CD的中点,F是A1D1的中点.(1)求异面直线AB1,BF所成角的余弦值,
(2)求三棱锥E-AB1D的体积.
分析 (1)建立如图所示的坐标系,确定$\overrightarrow{A{B}_{1}}$=(2,0,4),$\overrightarrow{BF}$=(-2,2,4),利用向量的夹角公式求异面直线AB1,BF所成角的余弦值,
(2)利用三棱锥的体积公式求三棱锥E-AB1D的体积.
解答  解:(1)建立如图所示的坐标系,则A(0,0,0),B1(2,0,4),B(2,0,0),F(0,2,4),
解:(1)建立如图所示的坐标系,则A(0,0,0),B1(2,0,4),B(2,0,0),F(0,2,4),
所以$\overrightarrow{A{B}_{1}}$=(2,0,4),$\overrightarrow{BF}$=(-2,2,4),
所以异面直线AB1,BF所成角的余弦值为$\frac{-4+16}{\sqrt{4+16}•\sqrt{4+4+16}}$=$\frac{\sqrt{30}}{10}$;
(2)在△CC1D中,由等面积可得C到平面AB1D的距离为$\frac{4×2}{\sqrt{20}}$=$\frac{4\sqrt{5}}{5}$,
所以E到平面AB1D的距离为$\frac{2\sqrt{5}}{5}$,
因为△AB1D的面积为$\frac{1}{2}×4×\sqrt{20}$=4$\sqrt{5}$,
所以三棱锥E-AB1D的体积为$\frac{1}{3}×4\sqrt{5}×\frac{2\sqrt{5}}{5}$=$\frac{8}{3}$.
点评 本题考查三棱锥体积的计算,考查异面直线AB1,BF所成角,正确运用向量法是关键.

练习册系列答案
相关题目
1.已知空间两条直线a、b没有公共点,则a和b( )
| A. | 一定是异面直线 | B. | 一定是平行直线 | ||
| C. | 不可能是平行直线 | D. | 不可能是相交直线 |
2.在△ABC中,若tan$\frac{A}{2}$,tan$\frac{B}{2}$,tan$\frac{C}{2}$成等比数列,则角B的取值范围是( )
| A. | (0,$\frac{π}{6}$] | B. | [$\frac{π}{3}$,$\frac{2π}{3}$] | C. | (0,$\frac{π}{3}$] | D. | [$\frac{2π}{3}$,π) |
 如图,BC是圆O的一条弦,延长BC至点E,使得BC=2CE=2,过E作圆O的切线,A为切点,∠BAC的平分线AD交BC于点D,则DE的长为$\sqrt{3}$.
如图,BC是圆O的一条弦,延长BC至点E,使得BC=2CE=2,过E作圆O的切线,A为切点,∠BAC的平分线AD交BC于点D,则DE的长为$\sqrt{3}$. 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=$\sqrt{3}$,BC=1,AA1=AC=2,E、F分别为A1C1、BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=$\sqrt{3}$,BC=1,AA1=AC=2,E、F分别为A1C1、BC的中点. 如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,BC∥AD且2BC=AD,∠PBC=90°,∠PBA≠90°.
如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,BC∥AD且2BC=AD,∠PBC=90°,∠PBA≠90°. 如图,在长方体ABCD-A1B1C1D1中,点E,F分别是棱AB,BC的中点,点E1,F1分别是棱A1D1,C1D1的中点.求证:EE1∥FF1.
如图,在长方体ABCD-A1B1C1D1中,点E,F分别是棱AB,BC的中点,点E1,F1分别是棱A1D1,C1D1的中点.求证:EE1∥FF1.