题目内容
9.f(x)=xsinx-cosx,f′(π)=-π.分析 根据函数的导数公式进行求解即可.
解答 解:函数的导数f′(x)=sinx+xcosx+sinx,
则f′(π)=sinπ+πcosπ+sinπ=-π,
故答案为:-π
点评 本题主要考查函数的导数的计算,根据导数公式是解决本题的关键.

练习册系列答案
相关题目
1.设函数f(x)的定义域为D,若函数f(x)满足条件,存在[a,b]⊆D,使得f(x)在区间[a,b]上的值域为[$\frac{a}{n}$,$\frac{b}{n}$](n∈N*),则称f(x)为“n倍缩函数”,若函数f(x)=log3(3x+t)位“3倍缩函数”,则t的取值范围为( )
| A. | (0,$\frac{1}{2}$) | B. | (0,$\frac{2\sqrt{3}}{9}$) | C. | (0,$\frac{\sqrt{3}}{3}$) | D. | (0,1) |
 如图,在四棱锥ABCD中,点E、F、G分别为棱BC、BD、CD的中点,且AB=AG,BC=BD.
如图,在四棱锥ABCD中,点E、F、G分别为棱BC、BD、CD的中点,且AB=AG,BC=BD.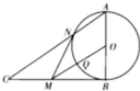 如图,在Rt△ABC中,∠ABC=90°,以AB为直径作圆O与斜边AB交于N,过点O作OM∥AC,交BC于M,交圆O于Q.
如图,在Rt△ABC中,∠ABC=90°,以AB为直径作圆O与斜边AB交于N,过点O作OM∥AC,交BC于M,交圆O于Q. 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=$\sqrt{3}$,BC=1,AA1=AC=2,E、F分别为A1C1、BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=$\sqrt{3}$,BC=1,AA1=AC=2,E、F分别为A1C1、BC的中点.