题目内容
3.如图1,等腰梯形ABCD中,BC∥AD,CE⊥AD,AD=3BC=3,CE=1,将△CDE沿CE折起得到四棱锥F-ABCE(如图2),G是AF的中点.(1)求证:BG∥平面FCE;
(2)当平面PCE⊥平面ABCE时,求三棱锥F-BEG的体积.

分析 (1)取EF中点H,连接GH,使得GH平行且等于$\frac{1}{2}$AE=1,证明四边形GHCB是平行四边形,可得BG∥CH,即可证明BG∥平面FCE;
(2)当平面PCE⊥平面ABCE时,EF⊥平面ABCE,利用分割法求三棱锥F-BEG的体积.
解答 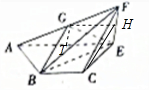 (1)证明:∵CE⊥AD,BC=1,AD=3,
(1)证明:∵CE⊥AD,BC=1,AD=3,
∴DE=1,AE=2,
取EF中点H,连接GH,使得GH平行且等于$\frac{1}{2}$AE=1,∴GH平行且等于BC,
∴四边形GHCB是平行四边形,
∴BG∥CH,
∵BG?平面FCE,CH?平面FCE,
∴BG∥平面FCE;
(2)当平面PCE⊥平面ABCE时,EF⊥平面ABCE.
S△ABE=$\frac{1}{2}AE•h$=$\frac{1}{2}×2×1$=1,
过G作GT⊥AE,则VG-ABE=$\frac{1}{3}×\frac{1}{2}×1$=$\frac{1}{6}$,VF-BCE=$\frac{1}{3}×\frac{1}{2}×1×1×1$=$\frac{1}{6}$,
∴VF-BEG=VF-ABCE-VG-ABE-VF-BCE=$\frac{1}{2}×1×\frac{(1+3)×1}{2}$-$\frac{1}{6}$-$\frac{1}{6}$=$\frac{2}{3}$.
点评 本题考查线面平行的判定,考查体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
13.下列等式成立的是( )
| A. | ${∫}_{a}^{b}$0dx=b-a | B. | ${∫}_{a}^{b}$xdx=$\frac{1}{2}$ | ||
| C. | ${∫}_{-1}^{1}$|x|dx=2${∫}_{0}^{1}$|x|dx | D. | ${∫}_{a}^{b}$(x+1)dx=${∫}_{a}^{b}$xdx |
15.已知直线l1:y=k1x+1和直线l2=kx2+b,则k1=k2”是“l1∥l2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |