题目内容
8.已知tan$\frac{α+β}{2}$=$\frac{\sqrt{6}}{2}$,tanα•tanβ=$\frac{13}{7}$,求cos(α-β)的值.分析 首先利用两角和与差的正切公式求出α,β的正切值,然后求差的正切值,从而得到所求.
解答 解:∵tan$\frac{α+β}{2}$=$\frac{\sqrt{6}}{2}$,
∴tan(α+β)=$\frac{2tan\frac{α+β}{2}}{1-ta{n}^{2}\frac{α+β}{2}}$=-2$\sqrt{6}$,
∵tanα•tanβ=$\frac{13}{7}$①,
∴由tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$,
即-2$\sqrt{6}$=$\frac{tanα+tanβ}{1-\frac{13}{7}}$,
∴tanα+tanβ=$\frac{12\sqrt{6}}{7}$②,
∴联立①②可得tanα=$\frac{6\sqrt{6}±5\sqrt{5}}{7}$,tanβ=$\frac{6\sqrt{6}\overline{+}5\sqrt{5}}{7}$,
所以tan(α-β)=$\frac{tanα-tanβ}{1+tanαtanβ}$═±$\frac{\sqrt{5}}{2}$,
所以cos(α-β)=±$\frac{1}{\sqrt{1+ta{n}^{2}(α-β)}}$=$±\frac{1}{\sqrt{1+\frac{5}{4}}}$=±$\frac{2}{3}$;
故答案为:±$\frac{2}{3}$.
点评 本题考查了两角和与差的正切公式的运用求三角函数的值,熟练掌握公式是关键,属于基本知识的考查.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
18.下列命题中,真命题是( )
| A. | ?x0∈R,e${\;}^{{x}_{0}}$≤0 | B. | ?x∈R,2x>x2 | ||
| C. | 命题:若x≠y,则sinx≠siny逆否命题 | D. | a>1,b>1是ab>1的充分不必要条件 |
 如图圆C半径为1,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|\overrightarrow{AB}-t\overrightarrow{AC}|≥|\overrightarrow{BC}|$对任意t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=1.
如图圆C半径为1,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|\overrightarrow{AB}-t\overrightarrow{AC}|≥|\overrightarrow{BC}|$对任意t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=1.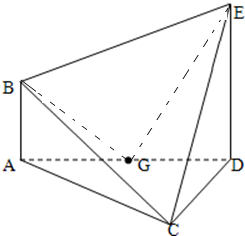 在如图所示的多面体ABCDE中,AB⊥平面ACD,AB∥DE,AD=DE=2CD=2,四边形ABED的面积为3,∠CAD=30°.
在如图所示的多面体ABCDE中,AB⊥平面ACD,AB∥DE,AD=DE=2CD=2,四边形ABED的面积为3,∠CAD=30°.