题目内容
数列{an}满足an+1+(-1)nan=2n-1,则{an}的前60项和为( )
| A.3690 | B.3660 | C.1845 | D.1830 |
D
∵an+1+(-1)nan=2n-1,
∴当n=2k(k∈N*)时,a2k+1+a2k=4k-1①
当n=2k+1(k∈N)时,a2k+2-a2k+1=4k+1②
①+②得:a2k+a2k+2=8k.
则a2+a4+a6+a8+…+a60=(a2+a4)+(a6+a8)+…+(a58+a60)=8(1+3+…+29)=8×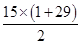 =1800.
=1800.
由②得a2k+1=a2k+2-(4k+1),
所以a1+a3+a5+…+a59=a2+a4+…+a60-[4×(0+1+2+…+29)+30]=1800-(4×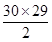 +30)=30,
+30)=30,
∴a1+a2+…+a60=1800+30=1830.
∴当n=2k(k∈N*)时,a2k+1+a2k=4k-1①
当n=2k+1(k∈N)时,a2k+2-a2k+1=4k+1②
①+②得:a2k+a2k+2=8k.
则a2+a4+a6+a8+…+a60=(a2+a4)+(a6+a8)+…+(a58+a60)=8(1+3+…+29)=8×
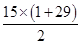 =1800.
=1800.由②得a2k+1=a2k+2-(4k+1),
所以a1+a3+a5+…+a59=a2+a4+…+a60-[4×(0+1+2+…+29)+30]=1800-(4×
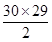 +30)=30,
+30)=30,∴a1+a2+…+a60=1800+30=1830.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
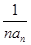 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.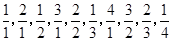 ,…,依它的前10项的规律,则a99+a100的值为( )
,…,依它的前10项的规律,则a99+a100的值为( )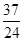
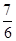
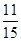

 <-1,且它的前n项和Sn有最大值,则使得Sn<0的n的最小值为( )
<-1,且它的前n项和Sn有最大值,则使得Sn<0的n的最小值为( )