题目内容
17.下列说法中不正确的是( )| A. | 若命题p:?x0∈R,使得x02-x0+1<0,则¬p:?x∈R,都有x2-x+1≥0. | |
| B. | 存在无数个α、β∈R,使得等式sin(α-β)=sinαcosβ+cosαsinβ成立 | |
| C. | 命题“在△ABC中,若sinA=sinB,则A=B”的逆否命题是真命题 | |
| D. | “p∧q为真”是“p∨q为真”的必要不充分条件 |
分析 (A)利用命题否定定义即可判断出正误;
(B)利用正弦的和差公式验证即可.
(C)有原命题的真假判断逆否命题的真假.
(D)利用联接词的真假判断来判断.
解答 解:(A)命题p:?x0∈R,使得x02-x0+1<0,则¬p:?x∈R,均有x2-x+1≥0,正确;
(B)sin(α-β)=sinαcosβ-sinβcosα=sinαcosβ+cosαsinβ.可得sinβcosα=0,所以只要β=kπ,α任意,或者α=2kπ+$\frac{π}{2}$,β任意.故B正确.
(C)“在△ABC中,若sinA=sinB,则A=B”为真命题,则其逆否命题为真命题.故C正确.
(D)“p且q”为真,则p,q同时为真,所以“p或q”为真,反之则不成立,
故“p且q”为真是“p或q”为真的充分不必要条件.故D错误.
故选:D
点评 本题主要考查存在性命题的否定、正弦和差公式、原命题与逆否命题的真假判断、联接词的真假判断等知识点,考查范围大,是高考常考题型.

练习册系列答案
相关题目
20.已知P是△ABC所在平面外一点,若P到ABC三边距离相等,则点P在平面ABC上的射影一定是△ABC的( )
| A. | 重心 | B. | 外心 | C. | 内心 | D. | 垂心 |
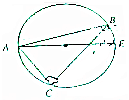 如图,已知,AE是⊙O的直径,弦BC与AE相交于D,求证:tanB•tanC=$\frac{AD}{DE}$.
如图,已知,AE是⊙O的直径,弦BC与AE相交于D,求证:tanB•tanC=$\frac{AD}{DE}$.