��Ŀ����
8����ͼ����ABC�У�D��E�ֱ�ΪAB��AC���е㣬CD��BE����F����$\overrightarrow{AB}$=$\overrightarrow{a}$��$\overrightarrow{AC}$=$\overrightarrow{b}$��$\overrightarrow{AF}$=m$\overrightarrow{a}$+n$\overrightarrow{b}$����m+n=��������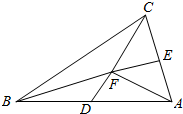
| A�� | 1 | B�� | $\frac{4}{3}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{5}{6}$ |
���� �ӳ�AF��BC�ڵ�M������AD=DB��AE=EC��CD��BE����F����֪����F�ǡ�ABC�����ģ��������������ĵ����ʺ�������ƽ���ı��η��ɵó���
��� 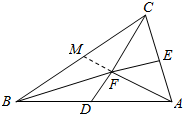 �⣺��ͼ��ʾ��
�⣺��ͼ��ʾ��
�ӳ�AF��BC�ڵ�M��
��AD=DB��AE=EC��CD��BE����F��
���F�ǡ�ABC�����ģ�
��$\overrightarrow{AF}$=$\frac{2}{3}\overrightarrow{AM}$��$\overrightarrow{AM}$=$\frac{1}{2}$��$\overrightarrow{AB}$+$\overrightarrow{AC}$����
��$\overrightarrow{AF}$=$\frac{1}{3}$��$\overrightarrow{AB}$+$\overrightarrow{AC}$��=$\frac{1}{3}$$\overrightarrow{a}$$+\frac{1}{3}\overrightarrow{b}$��
��$\overrightarrow{AF}$=m$\overrightarrow{a}$+n$\overrightarrow{b}$��
��m=n=$\frac{1}{3}$��
��m+n=$\frac{2}{3}$��
��ѡ��C��
���� ���⿼�������������ĵ����ʺ�������ƽ���ı��η������ڻ����⣮

��ϰ��ϵ�д�
�����Ŀ
19����f��x��=$\frac{1}{2}$��x+|x|������f��f��x�����ǣ�������
| A�� | x+|x| | B�� | 0 | C�� | $\left\{\begin{array}{l}{x��x��0}\\{0��x��0}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x��x��0}\\{0��x��0}\end{array}\right.$ |
16������ʽ��x2-$\frac{2}{\sqrt{x}}$��5��չ��ʽ�г������ǣ�������
| A�� | -32 | B�� | 32 | C�� | 80 | D�� | -80 |
20������x2-6px+p2=0������ʵ����x1��x2����$\frac{1}{{x}_{1}+p}$+$\frac{1}{{x}_{2}+p}$��ֵΪ��������
| A�� | p | B�� | -p | C�� | -$\frac{1}{p}$ | D�� | $\frac{1}{p}$ |