题目内容
【题目】已知函数![]()
![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)记函数![]() 的图象为曲线
的图象为曲线![]() .设点
.设点![]() ,
,![]() 是曲线
是曲线![]() 上的不同两点.如果在曲线
上的不同两点.如果在曲线![]() 上存在点
上存在点![]() ,使得:①
,使得:①![]() ;②曲线
;②曲线![]() 在点
在点![]() 处的切线平行于直线
处的切线平行于直线![]() ,则称函数
,则称函数![]() 存在“中值相依切线”.试问:函数
存在“中值相依切线”.试问:函数![]() 是否存在“中值相依切线”,请说明理由.
是否存在“中值相依切线”,请说明理由.
【答案】(I)当![]() 时, 函数
时, 函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减,当
上单调递减,当![]() 时, 函数
时, 函数![]() 在
在![]() 上单调递增,当
上单调递增,当![]() 时, 函数
时, 函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(II)不存在,理由见解析.
上单调递减;(II)不存在,理由见解析.
【解析】
试题分析:(I)求导得 ,按照两根大小来分类讨论,从而得到单调区间;(II)先假设存在,求出
,按照两根大小来分类讨论,从而得到单调区间;(II)先假设存在,求出![]() ,求出
,求出![]() ,由此化简得
,由此化简得![]() ,令
,令![]() 换元后化简得
换元后化简得![]() ,用导数证明不存在
,用导数证明不存在![]() 使上式成立.
使上式成立.
试题解析:
(Ⅰ)易知函数![]() 的定义域是
的定义域是![]() ,
,
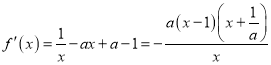
①当![]() 时,即
时,即![]() 时, 令
时, 令![]() ,解得
,解得![]() 或
或![]() ;
;
令![]() ,解得
,解得![]()
所以,函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
②当![]() 时,即
时,即![]() 时, 显然,函数
时, 显然,函数![]() 在
在![]() 上单调递增;
上单调递增;
③当![]() 时,即
时,即![]() 时, 令
时, 令![]() ,解得
,解得![]() 或
或![]() ;
;
令![]() ,解得
,解得![]() .
.
所以,函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
综上所述,
⑴当![]() 时, 函数
时, 函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
⑵当![]() 时, 函数
时, 函数![]() 在
在![]() 上单调递增;
上单调递增;
⑶当![]() 时, 函数
时, 函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
(Ⅱ)假设函数![]() 存在“中值相依切线”.
存在“中值相依切线”.
设![]() ,
,![]() 是曲线
是曲线![]() 上的不同两点,且
上的不同两点,且![]() ,
,
则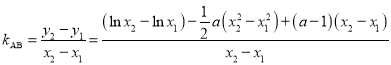
![]()
曲线在点![]() 处的切线斜率
处的切线斜率
![]() ,
,
依题意得:![]() .
.
化简可得:![]() ,即
,即 .
.
设![]() (
(![]() ),上式化为:
),上式化为:![]() , 即
, 即![]() .
.
令![]() ,
,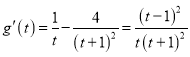 .
.
因为![]() ,显然
,显然![]() ,所以
,所以![]() 在
在![]() 上递增,显然有
上递增,显然有![]() 恒成立.
恒成立.
所以在![]() 内不存在
内不存在![]() ,使得
,使得![]() 成立.
成立.
综上所述,假设不成立.所以,函数![]() 不存在“中值相依切线”
不存在“中值相依切线”

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
