题目内容
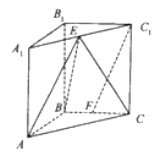
【题目】如图,在直角三棱柱![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)若直线![]() 和平面
和平面![]() 所成角的正弦值等于
所成角的正弦值等于![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)如图所示,取AB的中点M,连接MF,利用三角形中位线定理及其培训说不定判定定理可得四边形MFC1E是平行四边形,于是C1F∥EM,再利用线面平行的判定定理即可判断出结论;
(2)由直三棱柱ABC﹣A1B1C1,可得BB1⊥底面ABC,BB1⊥AB,再利用线面垂直的判定定理面面垂直的判定定理即可证明结论;
(3)由(2)可知:AB⊥BC.可建立如图所示的空间直角坐标系.求出平面ABE和平面CBE的法向量,代入公式,即可得到结果.
(1)证明:如图所示,取AB的中点M,连接MF,
则MF![]() AC,又EC1
AC,又EC1![]() AC,
AC,
∴EC1![]() MF,
MF,
∴四边形MFC1E是平行四边形,
∴C1F∥EM,又C1F平面ABE;
EM平面ABE;
∴C1F∥平面ABE.
(2)证明:由直三棱柱ABC﹣A1B1C1,∴BB1⊥底面ABC,
∴BB1⊥AB,又C1F⊥AB,BB1与C1F相交,
∴AB⊥平面ABE,又AB平面ABE,
∴平面ABE⊥平面B1BCC1;
(3)解:由(2)可知:AB⊥BC.
因此可建立如图所示的空间直角坐标系.F(0,1,0),设C1(0,2,t)(t>0),![]() (0,1,t).
(0,1,t).
由题意可取平面ACC1A1的法向量为![]() (1,1,0).
(1,1,0).
∵直线C1F和平面ACC1A1所成角的正弦值等于![]() ,
,
∴![]() |cos
|cos![]() |
|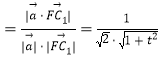 ,
,
解得t=2.
∴E(1,1,2),A(2,0,0),C(0,2,0),![]() (2,0,0),
(2,0,0),![]() (1,1,2),
(1,1,2),![]() (0,2,0).
(0,2,0).
设平面ABE的法向量为![]() (x,y,z),则
(x,y,z),则![]()
![]() 0,
0,
可得:x=0,x+y+2z=0,取y=2,可得:![]() (0,2,﹣1).
(0,2,﹣1).
同理可得平面CBE的法向量为![]() (2,0,﹣1).
(2,0,﹣1).
∴cos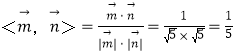 .
.
∴二面角A﹣BE﹣C的余弦值为![]() .
.