题目内容
【题目】为了弘扬传统文化，某市举办了“高中生诗词大赛”，现从全市参加比赛的学生中随机抽取
人的成绩进行统计，得到如图所示的频率分布直方图，其中成绩的分组区间为
，
，
，
.
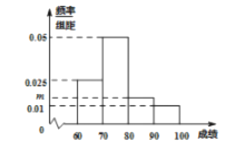
（1）求频率分布直方图中
的值；
（2）在所抽取的名学生中，用分层抽样的方法在成绩为
的学生中抽取了一个容量为
的样本，再从该样本中任意抽取
人，求人的成绩均在区间内的概率；
（3）若该市有
名高中生参赛，根据此次统计结果，试估算成绩在区间内的人数.
【答案】（1）0.015；（2）
；（3）1000.
【解析】
（1）由各组频率之和，即频率分布直方图中各组矩形的面积和为1，可得
的值；
（2）根据分层抽样的原则，可得成绩在
分别是3人和2人，之和写出抽取两人对应的所有的基本事件总数，找出满足条件的基本事件数，代入古典概型概率计算公式，可得答案；
（3）根据成绩落在
内的频率，可估算出成绩在区间的人数.
（1）依题意可知组距为
，
由
解得
.
（2）抽取了一个容量为
的样本成绩在区间
的人数为：
人，记3人为
、
、
.
成绩在区间的人数为：
人，记2人为
、
任取2人的基本事件为：
、
、
、
、
、
、
、
、
、
，共计10个.
其中在区间
的基本事件为： ，共计1个
所以
人的成绩均在区间的概率为：
.
（3）由
人，
即估计成绩在区间的人数为
人.
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目
