Question

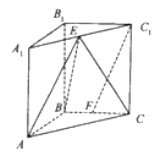
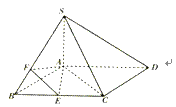
【题目】如图所示，四棱锥S﹣ABCD中，四边形ABCD为平行四边形，BA⊥AC，SA⊥AD，SC⊥CD．

（Ⅰ）求证：AC⊥SB；

（Ⅱ）若AB＝AC＝SA＝3，E为线段BC的中点，F为线段SB上靠近B的三等分点，求直线SC与平面AEF所成角的正弦值．

Answer 1

【答案】（Ⅰ）见解析（Ⅱ）

【解析】

（Ⅰ）由线面垂直的判定定理证明AC⊥平面SAB，即可证得AC⊥SB.

（Ⅱ）以AB、AC、AS为x轴y轴z轴建立坐标系，用向量法求解即可.

（Ⅰ）∵四边形ABCD为平行四边形，∴BA∥CD，

又BA⊥AC，∴CD⊥AC，

又SC⊥CD，AC∩SC＝C，∴CD⊥平面SAC，

又SA平面SAC，∴CD⊥SA，又SA⊥AD，CD∩AD＝D，

∴SA⊥平面ABCD，AC平面ABCD，∴SA⊥AC，

又BA⊥AC，SA∩BA＝A，∴AC⊥平面SAB，

又SB平面SAB，∴AC⊥SB．

（Ⅱ）以AB、AC、AS为x轴y轴z轴建立如图所示坐标系，

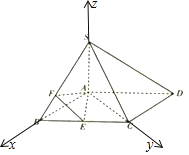
则A（0，0，0），S（0，0，3），C（0，3，0），E（，，0），F（2，0，1），

∴＝（，，0），＝（2，0，1），＝（0，﹣3，3），

设＝（x，y，z）为平面AEF的法向量，

，∴，∴，

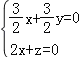令x＝﹣1，得一个法向量＝（﹣1，1，2），

cos＜，＞＝＝＝

即直线SC与平面AEF所成角的正弦值为．