题目内容
【题目】已知函数![]()
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在定义域上具有单调性,求实数
在定义域上具有单调性,求实数![]() 的取值范围;
的取值范围;
(3)求证: ![]()
【答案】(1)![]() (2)a≤2.(3)详见解析
(2)a≤2.(3)详见解析
【解析】试题分析:(1)由导数几何意义得切线斜率等于该点处导数值,再利用点斜式求切线方程,(2)先按单调递增与单调递减分类讨论,再将函数单调性转化为函数导数值恒非负或非正,利用变量分离转化为求对应函数最值,进而确定实数![]() 的取值范围;(3)利用导数证明数列求和不等式,一般方法为先构造目标函数(利用前面小题的结论),再代入数列,利用裂项相消法放缩求和,进而得证不等式.
的取值范围;(3)利用导数证明数列求和不等式,一般方法为先构造目标函数(利用前面小题的结论),再代入数列,利用裂项相消法放缩求和,进而得证不等式.
试题解析:(1)当a=1时,f(x)=(x+1)lnx﹣x+2,(x>0),
f′(x)=lnx+![]() ,f′(1)=1,f(1)=1,
,f′(1)=1,f(1)=1,
所以求在x=1处的切线方程为:y=x
(2)f′(x)=lnx+![]() +1﹣a,(x>0).
+1﹣a,(x>0).
(i)函数f(x)在定义域上单调递减时,
即a≥lnx+![]() 时,令g(x)=lnx+
时,令g(x)=lnx+![]() ,
,
当x>ea时,g′(x)>0,不成立;
(ii)函数f(x)在定义域上单调递增时,a≤lnx+![]() ;
;
令g(x)=lnx+![]() ,
,
则g′(x)=![]() ,x>0;
,x>0;
则函数g(x)在(0,1)上单调递减,在(1,+∞)上单调递增;
所以g(x)≥2,故a≤2.
(3)由(ii)得当a=2时f(x)在(1,+∞)上单调递增,
由f(x)>f(1),x>1得(x+1)lnx﹣2x+2>0,
即lnx>![]() 在(1,+∞)上总成立,
在(1,+∞)上总成立,
令x=![]() 得ln
得ln![]() >
>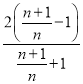 ,
,
化简得:ln(n+1)﹣lnn>![]() ,
,
所以ln2﹣ln1>![]() ,
,
ln3﹣ln2>![]() ,…,
,…,
ln(n+1)﹣lnn>![]() ,
,
累加得ln(n+1)﹣ln1>![]() ,
,
即![]() 命题得证.
命题得证.

 名校课堂系列答案
名校课堂系列答案【题目】某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果如下表所示:
休假次数 | 0 | 1 | 2 | 3 |
人数 | 5 | 10 | 20 | 15 |
根据表中信息解答以下问题:
(1)从该单位任选两名职工,求这两人休年假次数之和为4的概率;
(2)从该单位任选两名职工,用![]() 表示这两人休年假次数之差的绝对值,求随机变量
表示这两人休年假次数之差的绝对值,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.