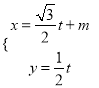题目内容
【题目】已知点![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() 是椭圆的焦点,直线
是椭圆的焦点,直线![]() 的斜率为
的斜率为![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,当
两点,当![]() 的面积最大时,求直线
的面积最大时,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)设出F,由直线AF的斜率为![]() ,求得c,结合离心率求得a,再由隐含条件求得b,则椭圆方程可求;
,求得c,结合离心率求得a,再由隐含条件求得b,则椭圆方程可求;
(2)当l⊥x轴时,不合题意;当直线l斜率存在时,设直线l:y=kx-2,联立直线方程和椭圆方程,由判别式大于0求得k的范围,再由弦长公式求得|PQ|,由点到直线的距离公式求得O到l的距离,代入三角形面积公式,化简后换元,利用基本不等式求得最值,进一步求出k值,则直线方程可求.
试题解析:
(1)设![]() ,解得
,解得![]() ,又
,又![]() ,
, ![]() 椭圆
椭圆![]() .
.
(2)当![]() 轴时,不合题意;当直线
轴时,不合题意;当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() ,联立
,联立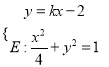 ,得
,得![]() ,由
,由![]() ,得
,得![]() ,即
,即![]() 或
或![]() ,
, ![]() ,从而
,从而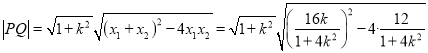
![]() ,又点
,又点![]() 到直线
到直线![]() 的距离
的距离![]() 的面积
的面积![]() ,设
,设![]() ,则
,则![]() ,
,
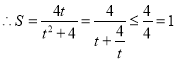 ,当且仅当
,当且仅当![]() ,即
,即![]() 时,等号成立,且
时,等号成立,且![]() ,此时
,此时![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目